【题目】已知：抛物线．

（1）写出抛物线的开口方向、对称轴；

（2）函数y有最大值还是最小值？并求出这个最大（小）值；

（3）设抛物线与y轴的交点为P，与x轴的交点为Q，求直线PQ的函数解析式．

参考答案：

【答案】解：（1）抛物线，

∵a= ＞0，

∴抛物线的开口向上，

对称轴为x=1；
（2）∵a=＞0，

∴函数y有最小值，最小值为－3；

（3）令x=0，则 ，

所以，点P的坐标为（0， ），

令y=0，则，

解得x1=-1，x2=3，

所以，点Q的坐标为（-1，0）或（3，0），

当点P（0， ），Q（-1，0）时，设直线PQ的解析式为y=kx+b，

则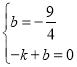 ，解得 k=， b= ，

所以直线PQ的解析式为 ，

当P（0， ），Q（3，0）时，设直线PQ的解析式为y=mx+n，

则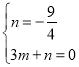 ，解得 m= ， n=- ，

所以，直线PQ的解析式为，

综上所述，直线PQ的解析式为或．

【解析】（1）根据二次函数的性质，写出开口方向与对称轴即可；

（2）根据a是正数确定有最小值，再根据函数解析式写出最小值；

（3）分别求出点P、Q的坐标，再根据待定系数法求函数解析式解答．

关闭