【题目】如图,一次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,过
,过![]() 的中点
的中点![]() 的直线
的直线![]() 交
交![]() 轴于点
轴于点![]() .
.

(1)求![]() ,
,![]() 两点的坐标及直线
两点的坐标及直线![]() 的函数表达式;
的函数表达式;
(2)若坐标平面内的点![]() ,能使以点
,能使以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形为平行四边形,请直接写出满足条件的点
为顶点的四边形为平行四边形,请直接写出满足条件的点![]() 的坐标.
的坐标.
参考答案:
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)点
;(2)点![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]() .
.
【解析】
(1)先根据一次函数![]() 求出A,B坐标,然后得到中点D的坐标,利用待定系数法求出直线CD的解析式即可求解;
求出A,B坐标,然后得到中点D的坐标,利用待定系数法求出直线CD的解析式即可求解;
(2)根据题意分3种情况,利用坐标平移的性质即可求解.
解:(1)一次函数![]() ,令
,令![]() ,则
,则![]() ;
;
令![]() ,则
,则![]() ,∴
,∴![]() ,
,![]() ,
,
∵![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,
设直线![]() 的函数表达式为
的函数表达式为![]() ,则
,则
![]() 解得
解得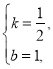
∴直线![]() 的函数表达式为
的函数表达式为![]() .
.
(2)①若四边形BCDF是平行四边形,则DF∥CB,DF=CB,
而点C向右平移6个单位长度得到点B,
∴点D向右平移6个单位长度得到点F(8,2);
②若四边形BCFD是平行四边形,则DF∥CB,DF=CB,
而点B向左平移6个单位长度得到点C,
∴点D向左平移6个单位长度得到点F(-4,2);
③若四边形BDCF是平行四边形,则BF∥DC,BF=DC,
而点D向左平移4个单位长度、向下平移2个单位长度得到点C,
∴点B向左平移4个单位长度、向下平移2个单位长度得到点F(0,-2);
综上,点![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为引导学生“爱读书,多读书,读好书”,某校七(2)班决定购买A、B两种书籍.若购买A种书籍1本和B种书籍3本,共需要180元;若购买A种书籍3本和B种书籍1本,共需要140元.
(1)求A、B两种书籍每本各需多少元?
(2)该班根据实际情况,要求购买A、B两种书籍总费用不超过700元,并且购买B种书籍的数量是A种书籍的
 ,求该班本次购买A、B两种书籍有哪几种方案?
,求该班本次购买A、B两种书籍有哪几种方案? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一个三角板放在边长为1的正方形
 上,并使它的直角顶点
上,并使它的直角顶点 在对角线
在对角线 上滑动,直角的一边始终经过点
上滑动,直角的一边始终经过点 ,另一边与射线
,另一边与射线 相交于点
相交于点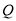 .
.
(1)当点
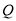 在
在 边上时,过点
边上时,过点 作
作 分别交
分别交 ,
, 于点
于点 ,
,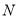 ,证明:
,证明: ;
;(2)当点
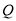 在线段
在线段 的延长线上时,设
的延长线上时,设 、
、 两点间的距离为
两点间的距离为 ,
, 的长为
的长为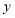 .
.①直接写出
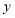 与
与 之间的函数关系,并写出函数自变量
之间的函数关系,并写出函数自变量 的取值范围;
的取值范围;②
 能否为等腰三角形?如果能,直接写出相应的
能否为等腰三角形?如果能,直接写出相应的 值;如果不能,说明理由.
值;如果不能,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:抛物线
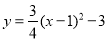 .
.(1)写出抛物线的开口方向、对称轴;
(2)函数y有最大值还是最小值?并求出这个最大(小)值;
(3)设抛物线与y轴的交点为P,与x轴的交点为Q,求直线PQ的函数解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知△ABC,点A的坐标是(4,0),点B的坐标是(2,3),点C在x轴的负半轴上,且AC=6.
(1)直接写出点C的坐标.
(2)在y轴上是否存在点P,使得S△POB=
 S△ABC若存在,求出点P的坐标;若不存在,请说明理由.
S△ABC若存在,求出点P的坐标;若不存在,请说明理由.(3)把点C往上平移3个单位得到点H,作射线CH,连接BH,点M在射线CH上运动(不与点C、H重合).试探究∠HBM,∠BMA,∠MAC之间的数量关系,并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】将一个正方形甲和两个正方形乙分别沿着图中虚线川剪刀剪成4个完全相等的长方形和一个正方形(如图1),已知正方形甲中剪出的小正方形面积是1,正方形乙中剪出的小正方形面积是4,现将剪得的12个长方形摆成如图2正方形
 (不重叠无缝隙).则正方形
(不重叠无缝隙).则正方形 的面积是()
的面积是()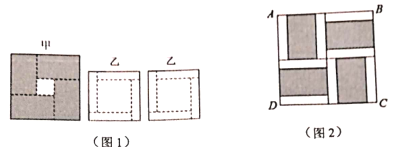
A.9B.16C.25D.36
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 ,
, ,求
,求 的度数.
的度数. 
(1)填空,在空白处填上结果或者理由.
解:过点
 作
作 ,(如图)
,(如图)得
 ___________°, ( )
___________°, ( )又因为
 ,(已知)
,(已知)所以
 ___________°.
___________°. 因为
 ,
,所以
 , ( )
, ( )又因为
 ,(已知)
,(已知)所以
 ___________°,
___________°,所以
 ___________°.
___________°. (2)请用另一种解法求
 的度数.
的度数.
相关试题

