练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，函数y=－a(x+a)与y=－ax2(a≠0)在同一坐标系上的图象是（）

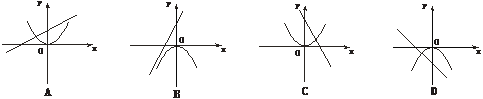
    A. A B. B C. C D. D

    【答案】D

    【解析】A选项中，抛物线开口向上说明a<0，则一次函数y=－a(x+a)=-ax-a2应该与y轴交于负半轴，所以A不正确；

    B选项中，抛物线开口向下说明a>0，则一次函数y=－a(x+a)=-ax-a2的图象应该从左至右下降，所以B不正确；

    C选项中，抛物线开口向上说明a<0，则一次函数y=－a(x+a)=-ax-a2的图象应该从左至右上升，所以C不正确；

    D选项中，抛物线开口向下说明a>0，则一次函数y=－a(x+a)=-ax-a2应该与y轴交于负半轴，且直线从左至右下降，所以D正确；

    故选D.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】下图是某汽车行驶的路程与时间（分钟）的函数关系图.

    观察图中所提供的信息，解答下列问题：

    （1）汽车在前分钟内的平均速度是 .

    （2）汽车在中途停了多长时间？

    （3）当时，求与的函数关系式

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，与都是等边三角形，、、三边长是一组勾股数，且边最长．

    （1）求证：

    （2）求的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，D、E分别是AB、AC的中点，过点E作EF∥AB，交BC于点F．

    （1）求证：四边形DBFE是平行四边形；

    （2）当△ABC满足什么条件时，四边形DBEF是菱形？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形OABC中，OA＝3，OC＝2，F是AB上的一个动点(F不与A，B重合)，过点F的反比例函数y＝ (x＞0)的图象与BC边交于点E.

    (1)当F为AB的中点时，求该函数的解析式；

    (2)当k为何值时，△EFA的面积最大，最大面积是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知一次函数y=ax+b的图象上有两点A、B，它们的横坐标分别是3，－1，若二次函数y=x2的图象经过A、B两点．

    （1）请求出一次函数的表达式；

    （2）设二次函数的顶点为C，求△ABC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，矩形ABCD中，对角线AC、BD交于O点，CE⊥BD于E，OF⊥AB 于F，BE：DE=1：3，OF=2cm，求AC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在菱形中，是边上一点，且，有下列结论：①；②是等边三角形；③是等腰三角形；④，其中结论正确的有_______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，已知△ABC的三个顶点坐标分别是A（1，1），B（4，1），C（3，3）．

    （1）将△ABC向下平移5个单位后得到△A1B1C1，请画出△A1B1C1；

    （2）将△ABC绕原点O逆时针旋转90°后得到△A2B2C2，请画出△A2B2C2；

    （3）判断以O，A1，B为顶点的三角形的形状．（无须说明理由）

    查看答案和解析>>

    同步练习册答案