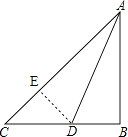
【题目】如图,为了测出旗杆AB的高度,在旗杆前的平地上选择一点C,测得旗杆顶部A的仰角为45°,在C、B之间选择一点D(C、D、B三点共线),测得旗杆顶部A的仰角为75°,且CD=8m 
(1)求点D到CA的距离;
(2)求旗杆AB的高.
(注:结果保留根号)
参考答案:
【答案】
(1)解:如图,作DE⊥AC于点E,
再Rt△CDE中,sinC= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴DE=4 ![]() ,
,
答:点D到CA的距离为4 ![]()
(2)解:在Rt△CDE中,∠C=45°,
∴△CDE为等腰直角三角形,
∴CE=DE=4 ![]() ,
,
∵∠ADB=75°,∠C=45°,
∴∠EAD=∠ADB﹣∠C=30°,
∴在Rt△ADE中,tan∠EAD= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴AE=4 ![]() ,
,
∴AC=AE+CE=4 ![]() +4
+4 ![]() ,
,
在Rt△ABC中,sinC= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴AB=4+4 ![]() ,
,
答:旗杆AB的高为(4+4 ![]() )m
)m
【解析】(1)作DE⊥AC于点E,根据sinC= ![]() 即可得DE;(2)由∠C=45°可得CE,由tan∠EAD=
即可得DE;(2)由∠C=45°可得CE,由tan∠EAD= ![]() 可得AE,即可得AC的长,再在Rt△ABC中,根据sinC=
可得AE,即可得AC的长,再在Rt△ABC中,根据sinC= ![]() 即可得AB的长.本题考查了解直角三角形,用到的知识点是仰角的定义、特殊角的三角函数值,要能借助仰角构造直角三角形并解直角三角形.
即可得AB的长.本题考查了解直角三角形,用到的知识点是仰角的定义、特殊角的三角函数值,要能借助仰角构造直角三角形并解直角三角形.
-
科目: 来源: 题型:
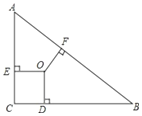
查看答案和解析>>【题目】已知,在△ABC中,∠ABC=90,点O为△ABC的三条角平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB,点D.E.F是垂足,且AB=17,BC=15,则OF、OE、OD的长度分别是( )
A. 2,2,2 B. 3,3,3 C. 4,4,4 D. 5,5,5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB//CD,BD平分∠ABC,∠2=∠3,BC⊥AC于C,DH⊥AB于H, DH交AC 于F,O是AB的中点,则下列说法正确的有( )

①BC=CD ②∠4=30° ③AH=HF ④OF//BD
A. ①②③ B. ②③④ C. ①②④ D. ①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,有一个等腰直角三角形AOB,∠OAB=90°,直角边AO在x轴上,且AO=1.将Rt△AOB绕原点O顺时针旋转90°得到等腰直角三角形A1OB1,且A1O=2AO,再将Rt△A1OB1绕原点O顺时针旋转90°得到等腰三角形A2OB2,且A2O=2A1O…,依此规律,得到等腰直角三角形A2017OB2017.则点B2017的坐标_______

-
科目: 来源: 题型:
查看答案和解析>>【题目】某宾馆拥有客房100间,经营中发现:每天入住的客房数y(间)与其价格x(元)(180≤x≤300)满足一次函数关系,部分对应值如表:
x(元)
180
260
280
300
y(间)
100
60
50
40
(1)求y与x之间的函数表达式;
(2)已知每间入住的客房,宾馆每日需支出各种费用100元;每日空置的客房需支出各种费用60元,当房价为多少元时,宾馆当日利润最大?求出最大值.(宾馆当日利润=当日房费收入﹣当日支出) -
科目: 来源: 题型:
查看答案和解析>>【题目】自学下面材料后,解答问题.
分母中含有未知数的不等式叫分式不等式.如:
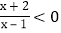 ;
;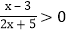 等.那么如何求出它们的解集呢?根据我们学过的有理数除法法则可知:两数相除,同号得正,异号得负.其字母表达式为:
等.那么如何求出它们的解集呢?根据我们学过的有理数除法法则可知:两数相除,同号得正,异号得负.其字母表达式为:(1)若
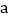 >0,
>0,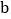 >0,则
>0,则 >0;若
>0;若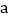 <0,
<0,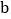 <0,则
<0,则 >0;
>0;(2)若
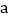 >0,
>0,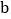 <0,则
<0,则 <0;若
<0;若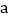 <0,
<0,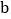 >0,则
>0,则 <0.
<0.反之:(1)若
 >0,则
>0,则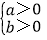 或
或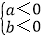
(2)若
 <0,则__________或__________.
<0,则__________或__________.(3)根据上述规律,求不等式
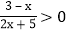 的解集.
的解集.(4)试求不等式
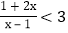 的解集.
的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将边长为6的正方形纸片ABCD对折,使AB与DC重合,折痕为EF,展平后,再将点B折到边CD上,使边AB经过点E,折痕为GH,点B的对应点为M,点A的对应点为N

(1)若CM=x,则CH=(用含x的代数式表示);
(2)求折痕GH的长.
相关试题

