【题目】如图,AB//CD,BD平分∠ABC,∠2=∠3,BC⊥AC于C,DH⊥AB于H, DH交AC 于F,O是AB的中点,则下列说法正确的有( )

①BC=CD ②∠4=30° ③AH=HF ④OF//BD
A. ①②③ B. ②③④ C. ①②④ D. ①③④
参考答案:
【答案】C
【解析】
根据平行线的性质可判定①;根据平行线的性质和角平分线的性质可得AD=BC=CD,从而∠4=∠3,再根据三角形的内角和即可求出∠4的度数据此判断②;根据∠3=30°可得AH与HF的关系即可判断③;连接OD,OE,O是AB中点,结合平行四边形的性质和等腰三角形的三线合一可得结论④.
解:∵AB//CD,BD平分∠ABC,
∴∠1=∠2=∠BDC,
∴BC=CD
①正确;
∵∠2=∠3,
∴∠DCA=∠CDB
∴BE=AE,CE=ED,梯形ABCD为等腰梯形,AD=BC=CD,
∴∠4=∠DCA=∠3;
在三角形ABC中,∠1+∠2+∠3=90°
∴∠4=∠DCA=∠3=30°
故②正确.
∠3=30°,
∴AH:HF=![]() :1,
:1,
故③错误;
连接OD,OE,O是AB中点,
∴OE⊥AB,BC=BO=CD,
∴四边形BCDO为平行四边形,
∴OD=BC=AD,DH⊥AB,三线合一,DH垂直平分AO,
∴∠FOA=∠FAO=30°=∠2,
∴OF//BD,
故④正确.
综上可知选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=90°,∠BAC=60°,△ACD是等边三角形,E是AC的中点,连接BE并延长,交DC于点F,求证:
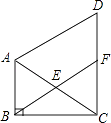
(1)△ABE≌△CFE;
(2)四边形ABFD是平行四边形. -
科目: 来源: 题型:
查看答案和解析>>【题目】小丽购买学习用品的收据如表,因污损导致部分数据无法识别,根据下表,解决下列问题:
(1)小丽买了自动铅笔、记号笔各几支?
(2)若小丽再次购买软皮笔记本和自动铅笔两种文具,共花费15元,则有哪几种不同的购买方案?商品名
单价(元)
数量(个)
金额(元)
签字笔
3
2
6
自动铅笔
1.5
●
●
记号笔
4
●
●
软皮笔记本
●
2
9
圆规
3.5
1
●
合计
8
28
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,在△ABC中,∠ABC=90,点O为△ABC的三条角平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB,点D.E.F是垂足,且AB=17,BC=15,则OF、OE、OD的长度分别是( )
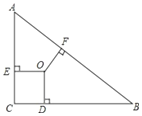
A. 2,2,2 B. 3,3,3 C. 4,4,4 D. 5,5,5
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,有一个等腰直角三角形AOB,∠OAB=90°,直角边AO在x轴上,且AO=1.将Rt△AOB绕原点O顺时针旋转90°得到等腰直角三角形A1OB1,且A1O=2AO,再将Rt△A1OB1绕原点O顺时针旋转90°得到等腰三角形A2OB2,且A2O=2A1O…,依此规律,得到等腰直角三角形A2017OB2017.则点B2017的坐标_______

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,为了测出旗杆AB的高度,在旗杆前的平地上选择一点C,测得旗杆顶部A的仰角为45°,在C、B之间选择一点D(C、D、B三点共线),测得旗杆顶部A的仰角为75°,且CD=8m

(1)求点D到CA的距离;
(2)求旗杆AB的高.
(注:结果保留根号) -
科目: 来源: 题型:
查看答案和解析>>【题目】某宾馆拥有客房100间,经营中发现:每天入住的客房数y(间)与其价格x(元)(180≤x≤300)满足一次函数关系,部分对应值如表:
x(元)
180
260
280
300
y(间)
100
60
50
40
(1)求y与x之间的函数表达式;
(2)已知每间入住的客房,宾馆每日需支出各种费用100元;每日空置的客房需支出各种费用60元,当房价为多少元时,宾馆当日利润最大?求出最大值.(宾馆当日利润=当日房费收入﹣当日支出)
相关试题

