【题目】自学下面材料后,解答问题.
分母中含有未知数的不等式叫分式不等式.如:![]() ;
;![]() 等.那么如何求出它们的解集呢?根据我们学过的有理数除法法则可知:两数相除,同号得正,异号得负.其字母表达式为:
等.那么如何求出它们的解集呢?根据我们学过的有理数除法法则可知:两数相除,同号得正,异号得负.其字母表达式为:
(1)若![]() >0,
>0,![]() >0,则
>0,则![]() >0;若
>0;若![]() <0,
<0,![]() <0,则
<0,则![]() >0;
>0;
(2)若![]() >0,
>0,![]() <0,则
<0,则![]() <0;若
<0;若![]() <0,
<0,![]() >0,则
>0,则![]() <0.
<0.
反之:(1)若![]() >0,则
>0,则![]() 或
或![]()
(2)若![]() <0,则__________或__________.
<0,则__________或__________.
(3)根据上述规律,求不等式![]() 的解集.
的解集.
(4)试求不等式![]() 的解集.
的解集.
参考答案:
【答案】![]()
![]()
【解析】
(2)根据两数相除,异号得负解答;
(3)先根据同号得正把不等式转化成不等式组,然后根据一元一次不等式组的解法求解即可;
(4) 先根据异号得负把不等式转化成不等式组,然后根据一元一次不等式组的解法求解即可.
(2)根据阅读,可以知道,![]() <0,所以,
<0,所以,![]() 、
、![]() 异号,
异号,
所以有![]() 或
或![]() 两种情况.
两种情况.
(3)∵![]()
∴![]() 或②
或②![]()
解一元一次不等式组,
得到①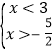 ,∴
,∴![]() ;
;
由②得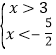 (无解)
(无解)
故不等式![]() 的解集为
的解集为![]()
(4)对不等式![]() 进行整理得到,
进行整理得到,![]() ,即
,即![]()
整理可得,![]()
∴![]() 或
或![]()
由①解得![]() ,∴
,∴![]()
由②解得![]() ,∴
,∴![]()
综上所述,不等式![]() 的解集为
的解集为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,有一个等腰直角三角形AOB,∠OAB=90°,直角边AO在x轴上,且AO=1.将Rt△AOB绕原点O顺时针旋转90°得到等腰直角三角形A1OB1,且A1O=2AO,再将Rt△A1OB1绕原点O顺时针旋转90°得到等腰三角形A2OB2,且A2O=2A1O…,依此规律,得到等腰直角三角形A2017OB2017.则点B2017的坐标_______

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,为了测出旗杆AB的高度,在旗杆前的平地上选择一点C,测得旗杆顶部A的仰角为45°,在C、B之间选择一点D(C、D、B三点共线),测得旗杆顶部A的仰角为75°,且CD=8m

(1)求点D到CA的距离;
(2)求旗杆AB的高.
(注:结果保留根号) -
科目: 来源: 题型:
查看答案和解析>>【题目】某宾馆拥有客房100间,经营中发现:每天入住的客房数y(间)与其价格x(元)(180≤x≤300)满足一次函数关系,部分对应值如表:
x(元)
180
260
280
300
y(间)
100
60
50
40
(1)求y与x之间的函数表达式;
(2)已知每间入住的客房,宾馆每日需支出各种费用100元;每日空置的客房需支出各种费用60元,当房价为多少元时,宾馆当日利润最大?求出最大值.(宾馆当日利润=当日房费收入﹣当日支出) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将边长为6的正方形纸片ABCD对折,使AB与DC重合,折痕为EF,展平后,再将点B折到边CD上,使边AB经过点E,折痕为GH,点B的对应点为M,点A的对应点为N

(1)若CM=x,则CH=(用含x的代数式表示);
(2)求折痕GH的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】某县为了落实中央的“强基惠民工程”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合做15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)已知甲队每天的施工费用为6500元,乙队每天的施工费用为3500元.为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙队合做来完成.则该工程施工费用是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图象经过点A(﹣1,0),B(0,﹣
 ),C(2,0),其对称轴与x轴交于点D
),C(2,0),其对称轴与x轴交于点D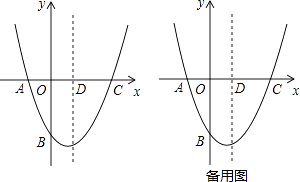
(1)求二次函数的表达式及其顶点坐标;
(2)若P为y轴上的一个动点,连接PD,则 PB+PD的最小值为;
PB+PD的最小值为;
(3)M(x,t)为抛物线对称轴上一动点
①若平面内存在点N,使得以A,B,M,N为顶点的四边形为菱形,则这样的点N共有 个;
②连接MA,MB,若∠AMB不小于60°,求t的取值范围.
相关试题

