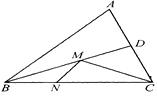
【题目】在锐角三角形ABC中.BC=![]() ,∠ABC=45°,BD平分∠ABC.若M,N分别是边BD,BC上的动点,则CM+MN的最小值是____.
,∠ABC=45°,BD平分∠ABC.若M,N分别是边BD,BC上的动点,则CM+MN的最小值是____.
参考答案:
【答案】4
【解析】
过点C作CE⊥AB于点E,交BD于点M′,过点M′作M′N′⊥BC于N′,则CE即为CM+MN的最小值,再根据BC=![]() ,∠ABC=45°,BD平分∠ABC可知△BCE是等腰直角三角形,由锐角三角函数的定义即可求出CE的长.
,∠ABC=45°,BD平分∠ABC可知△BCE是等腰直角三角形,由锐角三角函数的定义即可求出CE的长.
解:过点C作CE⊥AB于点E,交BD于点M′,过点M′作M′N′⊥BC于N′,
则CE即为CM+MN的最小值,
∵BC=![]() ,∠ABC=45°,BD平分∠ABC,
,∠ABC=45°,BD平分∠ABC,
∴△BCE是等腰直角三角形,
∴CE=BCcos45°=![]() ×
×![]() =4.
=4.
∴CM+MN的最小值为4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】春天来了,衢江河畔,鸟语花香,柳条摇曳.为给衢州市民提供更好的休闲锻炼环境,决定对衢江沿河步行道修建改造.据了解我市步行道改造工程路线约12千米,若该任务由甲、乙两工程队先后接力完成,甲工程队每天修建0.04千米,乙工程队每天修建0.02千米,则两工程队共需修建500天,求甲、乙两工程队分别修建步行道多少千米.
根据题意,小刚同学列出了一个不完整的方程组
 .
.(1)根据小刚同学所列的方程组,请你分别指出未知数
 ,
,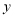 表示的意义.
表示的意义. 表示 ;
表示 ;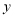 表示 ;
表示 ;(2)小红同学的做法是:“设甲工程队修建步行道
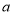 千米,乙工程队修建步行道
千米,乙工程队修建步行道 千米”,请你利用小红同学设的未知数解决问题.
千米”,请你利用小红同学设的未知数解决问题. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y1=ax2+bx﹣4(a≠0)与x轴交于点A(﹣1,0)和点B(4,0).
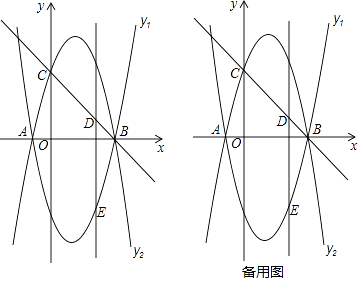
(1)求抛物线y1的函数解析式;
(2)如图①,将抛物线y1沿x轴翻折得到抛物线y2 , 抛物线y2与y轴交于点C,点D是线段BC上的一个动点,过点D作DE∥y轴交抛物线y1于点E,求线段DE的长度的最大值;
(3)在(2)的条件下,当线段DE处于长度最大值位置时,作线段BC的垂直平分线交DE于点F,垂足为H,点P是抛物线y2上一动点,⊙P与直线BC相切,且S⊙P:S△DFH=2π,求满足条件的所有点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CD∥AB,点O在AB上,OE平分∠BOD,OF⊥OE,∠D=110°.

(1)求∠DOE的度数;
(2)OF平分∠AOD吗?请说明理由.
-
科目: 来源: 题型:
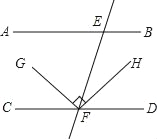
查看答案和解析>>【题目】如图,已知直线AB∥CD,FH平分∠EFD,FG⊥FH,∠AEF=62°,则∠GFC=_____度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=
 BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=
BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=  BC,成立的个数有( )
BC,成立的个数有( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中有一个△ABC,顶点A(﹣1,3),B(2,0),C(﹣3,﹣1).
(1)画出△ABC关于y轴的对称图形△A1B1C1(不写画法);
点A关于x轴对称的点坐标为
点B关于y轴对称的点坐标为
点C关于原点对称的点坐标为
(2)若网格上的每个小正方形的边长为1,则△ABC的面积是 .

相关试题

