【题目】如图,ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB= ![]() BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=
BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE= ![]() BC,成立的个数有( )
BC,成立的个数有( )
A.1个
B.2个
C.3个
D.4个
参考答案:
【答案】C
【解析】∵四边形ABCD是平行四边形,
∴∠ABC=∠ADC=60°,∠BAD=120°,
∵AE平分∠BAD,
∴∠BAE=∠EAD=60°
∴△ABE是等边三角形,
∴AE=AB=BE,
∵AB= ![]() BC,
BC,
∴AE= ![]() BC,
BC,
∴∠BAC=90°,
∴∠CAD=30°,故①正确;
∵AC⊥AB,
∴SABCD=ABAC,故②正确,
∵AB= ![]() BC,OB=
BC,OB= ![]() BD,
BD,
∵BD>BC,
∴AB≠OB,故③错误;
∵CE=BE,CO=OA,
∴OE= ![]() AB,
AB,
∴OE= ![]() BC,故④正确.
BC,故④正确.
故答案为:C.
首先根据平行四边形的性质可得到∠ABC=∠ADC=60°,∠BAD=120°,然后结合条件AE平分∠BAD,可得到∠BAE=∠EAD=60°,故此可证明△ABE是等边三角形,由于AB=![]() BC,得到AE=
BC,得到AE=![]() BC,得到△ABC是直角三角形,于是得到∠CAD=30°,故①正确;因为AC⊥AB,所以依据平行四边形的面积公式可得到SABCD=ABAC,故②正确,然后由AB=
BC,得到△ABC是直角三角形,于是得到∠CAD=30°,故①正确;因为AC⊥AB,所以依据平行四边形的面积公式可得到SABCD=ABAC,故②正确,然后由AB=![]() BC,OB=
BC,OB=![]() BD,且BD>BC,可证明AB≠OB,故③错误;接下来,依据三角形的中位线的性质定理证明OE=
BD,且BD>BC,可证明AB≠OB,故③错误;接下来,依据三角形的中位线的性质定理证明OE=![]() AB,于是得到OE=
AB,于是得到OE=![]() BC,故④正确.
BC,故④正确.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CD∥AB,点O在AB上,OE平分∠BOD,OF⊥OE,∠D=110°.

(1)求∠DOE的度数;
(2)OF平分∠AOD吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在锐角三角形ABC中.BC=
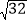 ,∠ABC=45°,BD平分∠ABC.若M,N分别是边BD,BC上的动点,则CM+MN的最小值是____.
,∠ABC=45°,BD平分∠ABC.若M,N分别是边BD,BC上的动点,则CM+MN的最小值是____.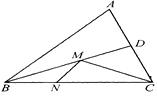
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线AB∥CD,FH平分∠EFD,FG⊥FH,∠AEF=62°,则∠GFC=_____度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中有一个△ABC,顶点A(﹣1,3),B(2,0),C(﹣3,﹣1).
(1)画出△ABC关于y轴的对称图形△A1B1C1(不写画法);
点A关于x轴对称的点坐标为
点B关于y轴对称的点坐标为
点C关于原点对称的点坐标为
(2)若网格上的每个小正方形的边长为1,则△ABC的面积是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】看图填空:已知如图,AD⊥BC于D,EG⊥BC于G,∠E=∠3, 求证:AD平分∠BAC.
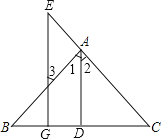
证明:∵AD⊥BC于D,EG⊥BC于G( 已知 )
∴∠ADC=90°,∠EGC=90°( )
∴∠ADC=∠EGC(等量代换)
∴AD∥EG( )
∴∠1=∠3( )
∠2=∠E( )
又∵∠E=∠3( 已知) ∴∠1=∠2( )
∴AD平分∠BAC( ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是半圆O的直径,点C是
 的中点,点D是
的中点,点D是 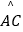 的中点,连接AC,BD交于点E,则
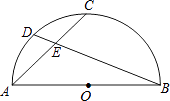
的中点,连接AC,BD交于点E,则 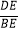 =( )
=( )
A.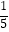
B.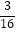
C.1﹣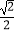
D.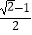
相关试题

