【题目】已知抛物线y1=ax2+bx﹣4(a≠0)与x轴交于点A(﹣1,0)和点B(4,0).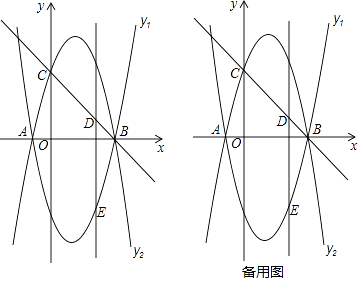
(1)求抛物线y1的函数解析式;
(2)如图①,将抛物线y1沿x轴翻折得到抛物线y2 , 抛物线y2与y轴交于点C,点D是线段BC上的一个动点,过点D作DE∥y轴交抛物线y1于点E,求线段DE的长度的最大值;
(3)在(2)的条件下,当线段DE处于长度最大值位置时,作线段BC的垂直平分线交DE于点F,垂足为H,点P是抛物线y2上一动点,⊙P与直线BC相切,且S⊙P:S△DFH=2π,求满足条件的所有点P的坐标.
参考答案:
【答案】
(1)解:将点A(﹣1,0)和点B(4,0)代入y1=ax2+bx﹣4得:a=1,b=﹣3,
∴抛物线y1的函数解析式为:y1=x2﹣3x﹣4;
(2)解:由对称性可知,抛物线y2的函数解析式为:y2=﹣x2+3x+4,
∴C(0,4),设直线BC的解析式为:y=kx+q,
把B(4,0),C(0,4)代入得,k=﹣1,q=4,
∴直线BC的解析式为:y=﹣x+4,
设D(m,﹣m+4),E(m,m2﹣3m﹣4),其中0≤m≤4,
∴DE=﹣m+4﹣(m2﹣3m﹣4)=﹣(m﹣1)2+9,
∵0≤m≤4,∴当m=1时,DEmax=9;
此时,D(1,3),E(1,﹣6);
(3)解:由题意可知,△BOC是等腰直角三角形,

∴线段BC的垂直平分线为:y=x,
由(2)知,直线DE的解析式为:x=1,
∴F(1,1),
∵H是BC的中点,
∴H(2,2),
∴DH= ![]() ,FH=
,FH= ![]() ,
,
∴S△DFH=1,
设⊙P的半径为r,
∵S⊙P:S△DFH=2π,
∴r= ![]() ,
,
∵⊙P与直线BC相切,
∴点P在与直线BC平行且距离为 ![]() 的直线上,
的直线上,
∴点P在直线y=﹣x+2或y=﹣x+6的直线上,
∵点P在抛物线y2=﹣x2+3x+4上,
∴﹣x+2=﹣x2+3x+4,
解得:x1=2+ ![]() ,x2=2﹣
,x2=2﹣ ![]() ,
,
﹣x+6=﹣x2+3x+4,
解得:x3=2+ ![]() ,x4=2﹣
,x4=2﹣ ![]() ,
,
∴符合条件的点P坐标有4个,分别是(2+ ![]() ,﹣
,﹣ ![]() ),(2﹣
),(2﹣ ![]() ,
, ![]() ),(2+
),(2+ ![]() ,4﹣
,4﹣ ![]() ),(2﹣
),(2﹣ ![]() ,4+
,4+ ![]() ).
).
【解析】(1)(1)把A(﹣1,0)和点B(4,0)坐标代入抛物线解析式,利用待定系数法即可求出;(2)关于x轴翻折后的解析式可套用点关于x轴对称坐标变换方法即x不变,y变为其相反数-y ,-y=x2﹣3x﹣4,即y2=﹣x2+3x+4;竖直线段的最值问题可以化归为函数最值问题,须构建以动点D的横坐标m为自变量,DE长为因变量的函数,竖直线段等于上、下两端点的纵坐标之差来表示,二次函数最值问题可用配方法解决;(3)利用互垂直线的斜率积=-1求出BC的垂直平分线的解析式,由S⊙P:S△DFH=2π,得r= ![]() ,,由⊙P与直线BC相切,可知点P在与直线BC平行且距离为
,,由⊙P与直线BC相切,可知点P在与直线BC平行且距离为 ![]() 的直线上,由点P在直线y=﹣x+2或y=﹣x+6的直线上,点P在抛物线y2=﹣x2+3x+4上,联立解析式﹣x+2=﹣x2+3x+4和﹣x+6=﹣x2+3x+4,分别解方程即可.
的直线上,由点P在直线y=﹣x+2或y=﹣x+6的直线上,点P在抛物线y2=﹣x2+3x+4上,联立解析式﹣x+2=﹣x2+3x+4和﹣x+6=﹣x2+3x+4,分别解方程即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(阅读材料)
我们知道,图形也是一种重要的数学语言,它直观形象,能有效地表现一些代数中的数量关系,而运用代数思想也能巧妙地解决一些图形问题.
在一次数学活动课上,张老师准备了若干张如图1所示的甲、乙、丙三种纸片,其中甲种纸片是边长为
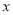 的正方形,乙种纸片是边长为
的正方形,乙种纸片是边长为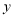 的正方形,丙种纸片是长为
的正方形,丙种纸片是长为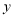 ,宽为
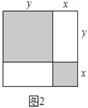
,宽为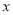 的长方形,并用甲种纸片一张,乙种纸片一张,丙种纸片两张拼成了如图2所示的一个大正方形.
的长方形,并用甲种纸片一张,乙种纸片一张,丙种纸片两张拼成了如图2所示的一个大正方形.(理解应用)
(1)观察图2,用两种不同方式表示阴影部分的面积可得到一个等式,请你直接写出这个等式.
(拓展升华)
(2)利用(1)中的等式解决下列问题.
①已知
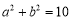 ,
,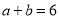 ,求
,求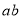 的值;
的值;②已知
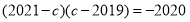 ,求
,求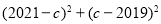 的值.
的值.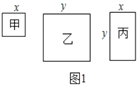
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,BC=a,AC=b,AB=c,设c为最长边,当a2+b2=c2时,△ABC是直角三角形;当a2+b2≠c2时,利用代数式a2+b2和c2的大小关系,探究△ABC的形状(按角分类).
(1)当△ABC三边分别为6、8、9时,△ABC为 三角形;当△ABC三边分别为6、8、11时,△ABC为 三角形.
(2)猜想,当a2+b2 c2时,△ABC为锐角三角形;当a2+b2 c2时,△ABC为钝角三角形.
(3)判断当a=2,b=4时,△ABC的形状,并求出对应的c的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】春天来了,衢江河畔,鸟语花香,柳条摇曳.为给衢州市民提供更好的休闲锻炼环境,决定对衢江沿河步行道修建改造.据了解我市步行道改造工程路线约12千米,若该任务由甲、乙两工程队先后接力完成,甲工程队每天修建0.04千米,乙工程队每天修建0.02千米,则两工程队共需修建500天,求甲、乙两工程队分别修建步行道多少千米.
根据题意,小刚同学列出了一个不完整的方程组
 .
.(1)根据小刚同学所列的方程组,请你分别指出未知数
 ,
,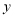 表示的意义.
表示的意义. 表示 ;
表示 ;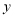 表示 ;
表示 ;(2)小红同学的做法是:“设甲工程队修建步行道
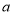 千米,乙工程队修建步行道
千米,乙工程队修建步行道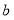 千米”,请你利用小红同学设的未知数解决问题.
千米”,请你利用小红同学设的未知数解决问题. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CD∥AB,点O在AB上,OE平分∠BOD,OF⊥OE,∠D=110°.

(1)求∠DOE的度数;
(2)OF平分∠AOD吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在锐角三角形ABC中.BC=
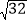 ,∠ABC=45°,BD平分∠ABC.若M,N分别是边BD,BC上的动点,则CM+MN的最小值是____.
,∠ABC=45°,BD平分∠ABC.若M,N分别是边BD,BC上的动点,则CM+MN的最小值是____.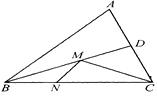
-
科目: 来源: 题型:
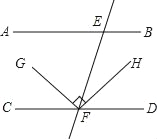
查看答案和解析>>【题目】如图,已知直线AB∥CD,FH平分∠EFD,FG⊥FH,∠AEF=62°,则∠GFC=_____度.
相关试题

