【题目】在△ABC中,角A、B、C的对边分别为a,b,c,且bcosC=(2a﹣c)cosB.
(1)求角B的大小;
(2)已知b= ![]() ,BD为AC边上的高,求BD的取值范围.
,BD为AC边上的高,求BD的取值范围.
参考答案:
【答案】
(1)解:由bcosC=(2a﹣c)cosB得b ![]() =(2a﹣c)
=(2a﹣c) ![]() ,
,
化简得a2+c2﹣b2=ac,∴cosB= ![]() ,
,
∵B∈(0,π),∴B= ![]() .
.
(2)解:设BD为AC边上的高为h,
∵s= ![]() ,∴h=
,∴h= ![]() =ac,
=ac,
由余弦定理得b2=a2+c2﹣2accosBa2+c2﹣ac=33≥2ac﹣ac,
∴ac≤3,∴h= ![]() =ac≤3.
=ac≤3.
故BD的取值范围为(0,3]
【解析】(1)由bcosC=(2a﹣c)cosB得a2+c2﹣b2=ac,∴cosB= ![]() ,即B=
,即B= ![]() .(2)设BD为AC边上的高为h由s=
.(2)设BD为AC边上的高为h由s= ![]() ,得h=
,得h= ![]() =ac,由余弦定理得b2=a2+c2﹣2accosB3≥2ac﹣ac,即ac≤3,即h=
=ac,由余弦定理得b2=a2+c2﹣2accosB3≥2ac﹣ac,即ac≤3,即h= ![]() =ac≤3,从而可得BD的取值范围
=ac≤3,从而可得BD的取值范围
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC 中,∠ACB=90°,AC=BC,AE 是 BC 边的中线,过点C 作 CF⊥AE,垂足为点 F,过点 B 作 BD⊥BC 交 CF 的延长线于点 D.
(1)试证明:AE=CD;
(2)若 AC=12cm,求线段 BD 的长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰梯形ABCD中,AB∥DC、CD=2AB=4,∠A=
 ,向量
,向量  、
、 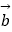 满足
满足 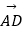 =2
=2  ,
,  =2
=2  +
+ 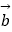 ,则下列式子不正确的是( )
,则下列式子不正确的是( )
A.|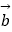 |=2
|=2
B.|2 |=2
|=2 
C.2 =﹣2
=﹣2
D. =1
=1 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an} 满足a1=
 ,a2=
,a2=  ,an+2﹣an+1=(﹣1)n+1(an+1﹣an)(n∈N*),数列{an}的前n项和为Sn , 则S2017= .
,an+2﹣an+1=(﹣1)n+1(an+1﹣an)(n∈N*),数列{an}的前n项和为Sn , 则S2017= . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在以A、B、C、D、E为顶点的五面体中,AD⊥平面ABC,AD∥BE,AC⊥CB,AB=2BE=4AD=4.

(1)O为AB的中点,F是线段BE上的一点,BE=4BF,证明:OF∥平面CDE;
(2)当直线DE与平面CBE所成角的正切值为 时,求平面CDE与平面ABC所成锐二面角的余弦值.
时,求平面CDE与平面ABC所成锐二面角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】2017年是某市大力推进居民生活垃圾分类的关键一年,有关部门为宣传垃圾分类知识,面向该市市民进行了一次“垃圾分类知识”的网络问卷调查,每位市民仅有一次参与机会,通过抽样,得到参与问卷调查中的1000人的得分数据,其频率分布直方图如图所示:

(1)由频率分布直方图可以认为,此次问卷调查的得分Z服从正态分布N(μ,210),μ近似为这1000人得分的平均值(同一组数据用该区间的中点值作代表),利用该正态分布,求P(50.5<Z<94).
(2)在(1)的条件下,有关部门为此次参加问卷调查的市民制定如下奖励方案: ①得分不低于μ可获赠2次随机话费,得分低于μ则只有1次;
②每次赠送的随机话费和对应概率如下:赠送话费(单位:元)
10
20
概率


现有一位市民要参加此次问卷调查,记X(单位:元)为该市民参加问卷调查获赠的话费,求X的分布列.
附: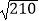 ≈14.5
≈14.5
若Z~N(μ,δ2),则P(μ﹣δ<Z<μ+δ)=0.6826,P(μ﹣2δ<Z<μ+2δ)=0.9544. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,△ABC的周长为12,AB,AC边的中点分别为F1(﹣1,0)和F2(1,0),点M为BC边的中点.
(1)求点M的轨迹方程;
(2)设点M的轨迹为曲线T,直线MF1与曲线T另一个交点为N,线段MF2中点为E,记S=S +S
+S  ,求S的最大值.
,求S的最大值.
相关试题

