【题目】如图,已知抛物线y= ![]() x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.
x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点. 
(1)求抛物线的解析式;
(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.
参考答案:
【答案】
(1)
解:∵点A(0,1).B(﹣9,10)在抛物线上,
∴ 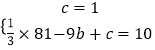 ,
,
∴ ![]() ,
,
∴抛物线的解析式为y= ![]() x2+2x+1
x2+2x+1
(2)
解:∵AC∥x轴,A(0,1)
∴ ![]() x2+2x+1=1,
x2+2x+1=1,
∴x1=6,x2=0,
∴点C的坐标(﹣6,1),
∵点A(0,1).B(﹣9,10),
∴直线AB的解析式为y=﹣x+1,
设点P(m, ![]() m2+2m+1)
m2+2m+1)
∴E(m,﹣m+1)
∴PE=﹣m+1﹣( ![]() m2+2m+1)=﹣
m2+2m+1)=﹣ ![]() m2﹣3m,
m2﹣3m,
∵AC⊥EP,AC=6,
∴S四边形AECP
=S△AEC+S△APC
= ![]() AC×EF+
AC×EF+ ![]() AC×PF
AC×PF
= ![]() AC×(EF+PF)
AC×(EF+PF)
= ![]() AC×PE
AC×PE
= ![]() ×6×(﹣
×6×(﹣ ![]() m2﹣3m)
m2﹣3m)
=﹣m2﹣9m
=﹣(m+ ![]() )2+
)2+ ![]() ,
,
∵﹣6<m<0
∴当m=﹣ ![]() 时,四边形AECP的面积的最大值是
时,四边形AECP的面积的最大值是 ![]() ,
,
此时点P(﹣ ![]() ,﹣
,﹣ ![]() ).
).
(3)
解:∵y= ![]() x2+2x+1=
x2+2x+1= ![]() (x+3)2﹣2,
(x+3)2﹣2,
∴P(﹣3,﹣2),
∴PF=yF﹣yP=3,CF=xF﹣xC=3,
∴PF=CF,
∴∠PCF=45°
同理可得:∠EAF=45°,
∴∠PCF=∠EAF,
∴在直线AC上存在满足条件的Q,
设Q(t,1)且AB=9 ![]() ,AC=6,CP=3
,AC=6,CP=3 ![]()
∵以C、P、Q为顶点的三角形与△ABC相似,
①当△CPQ∽△ABC时,
∴ ![]() ,
,
∴ ![]() ,
,
∴t=﹣4,
∴Q(﹣4,1)
②当△CQP∽△ABC时,
∴ ![]() ,
,
∴ ![]() ,
,
∴t=3,
∴Q(3,1).
【解析】(1)用待定系数法求出抛物线解析式即可;
(2)设点P(m, ![]() m2+2m+1),表示出PE=﹣
m2+2m+1),表示出PE=﹣ ![]() m2﹣3m,再用S四边形AECP=S△AEC+S△APC=
m2﹣3m,再用S四边形AECP=S△AEC+S△APC= ![]() AC×PE,建立函数关系式,求出极值即可;
AC×PE,建立函数关系式,求出极值即可;
(3)先判断出PF=CF,再得到∠PCF=∠EAF,以C、P、Q为顶点的三角形与△ABC相似,分两种情况计算即可.此题是二次函数综合题,主要考查了待定系数法,相似三角形的性质,几何图形面积的求法(用割补法),解本题的关键是求函数解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,在平面直角坐标系xOy中,点A、B、C分别为坐标轴上上的三个点,且OA=1,OB=3,OC=4,
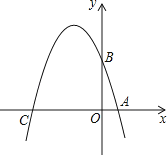
(1)求经过A、B、C三点的抛物线的解析式;
(2)在平面直角坐标系xOy中是否存在一点P,使得以以点A、B、C、P为顶点的四边形为菱形?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)若点M为该抛物线上一动点,在(2)的条件下,请求出当|PM﹣AM|的最大值时点M的坐标,并直接写出|PM﹣AM|的最大值. -
科目: 来源: 题型:
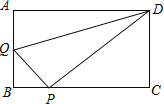
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=120°,AB=AC=4,AD⊥BC,BD=2
 ,延长AD到E,使AE=2AD,连接BE.
,延长AD到E,使AE=2AD,连接BE.(1)求证:△ABE为等边三角形;
(2)将一块含60°角的直角三角板PMN如图放置,其中点P与点E重合,且∠NEM=60°,边NE与AB交于点G,边ME与AC交于点F.求证:BG=AF;
(3)在(2)的条件下,求四边形AGEF的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),AB=4cm,AC⊥AB,BD⊥AB,AC=BD=3cm.点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为t(s).
(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,请说明理由,并判断此时线段PC和线段PQ的位置关系;
(2)如图(2),将图(1)中的“AC⊥AB,BD⊥AB”为改“∠CAB=∠DBA=60°”,其他条件不变.设点Q的运动速度为x cm/s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x、t的值;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,AB=3,AD=4,动点Q从点A出发,以每秒1个单位的速度,沿AB向点B移动;同时点P从点B出发,仍以每秒1个单位的速度,沿BC向点C移动,连接QP,QD,PD.若两个点同时运动的时间为x秒(0<x≤3),解答下列问题:
(1)设△QPD的面积为S,用含x的函数关系式表示S;当x为何值时,S有最大值?并求出最小值;
(2)是否存在x的值,使得QP⊥DP?试说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点O为坐标原点,直线l与抛物线y=mx2+nx相交于A(1,3
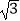 ),B(4,0)两点.
),B(4,0)两点. 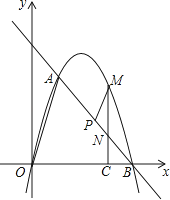
(1)求出抛物线的解析式;
(2)在坐标轴上是否存在点D,使得△ABD是以线段AB为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由;
(3)点P是线段AB上一动点,(点P不与点A、B重合),过点P作PM∥OA,交第一象限内的抛物线于点M,过点M作MC⊥x轴于点C,交AB于点N,若△BCN、△PMN的面积S△BCN、S△PMN满足S△BCN=2S△PMN , 求出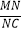 的值,并求出此时点M的坐标.
的值,并求出此时点M的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法错误的是()
A. 两个面积相等的圆一定全等
B. 全等三角形是指形状、大小都相同的三角形
C. 斜边上中线和一条直角边对应相等的两直角三角形全等
D. 底边相等的两个等腰三角形全等
相关试题

