【题目】如图(1),AB=4cm,AC⊥AB,BD⊥AB,AC=BD=3cm.点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为t(s).
(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,请说明理由,并判断此时线段PC和线段PQ的位置关系;
(2)如图(2),将图(1)中的“AC⊥AB,BD⊥AB”为改“∠CAB=∠DBA=60°”,其他条件不变.设点Q的运动速度为x cm/s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x、t的值;若不存在,请说明理由.

参考答案:
【答案】(1)全等,PC⊥PQ,理由参见解析;(2)存在,t=1,x="1" 或t=2,x=![]() .
.
【解析】试题分析:(1)利用SAS证得△ACP≌△BPQ,得出∠ACP=∠BPQ,进一步得出∠APC+∠BPQ=∠APC+∠ACP=90°得出结论即可;(2)由△ACP≌△BPQ,分两种情况:①AC=BP,AP=BQ,②AC=BQ,AP=BP,建立方程组求得答案即可.
试题解析:(1)当t=1时,AP=BQ=1,∵AB=4cm,∴BP=AC=3,又因为∠A=∠B=90°,∴△ACP≌△BPQ(SAS).∴∠ACP=∠BPQ,∴∠APC+∠BPQ=∠APC+∠ACP=90°.∴∠CPQ=90°,即线段PC与线段PQ垂直;(2)设点Q的运动速度为x cm/s,则BQ=tx,分两种情况:①若△ACP≌△BPQ,则AC=BP,AP=BQ,所以3=4-t,t=xt,解得:t=1,x=1;②若△ACP≌△BQP,则AC=BQ,AP=BP,所以3=xt,t=4-t,解得:t=2,x=![]() .综上所述,存在这样的实数x,使得△ACP与△BPQ全等,此时相应的x、t的值为t=1,x="1" 或t=2,x=
.综上所述,存在这样的实数x,使得△ACP与△BPQ全等,此时相应的x、t的值为t=1,x="1" 或t=2,x=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知下列命题: ①若
 >1,则a>b;
>1,则a>b;
②若a+b=0,则|a|=|b|;
③等边三角形的三个内角都相等;
④底角相等的两个等腰三角形全等.
其中原命题与逆命题均为真命题的个数是( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】从汽车灯的点O处发出的一束光线经灯的反光罩反射后沿CO方向平行射出,如入射光线OA的反射光线为AB,
 在如图中所示的截面内,若入射光线OD经反光罩反射后沿DE射出,且
在如图中所示的截面内,若入射光线OD经反光罩反射后沿DE射出,且 则
则 的度数是______.
的度数是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场对一种新售的手机进行市场问卷调查,其中一个项目是让每个人按
 不喜欢
不喜欢 、
、 一般
一般 、
、 不比较喜欢
不比较喜欢 、
、 非常喜欢
非常喜欢 四个等级对该手机进行评价,图
四个等级对该手机进行评价,图 和图
和图 是该商场采集数据后,绘制的两幅不完整的统计图,请你根据以上统计图提供的信息,回答下列问题:
是该商场采集数据后,绘制的两幅不完整的统计图,请你根据以上统计图提供的信息,回答下列问题: 本次调查的人数为多少人?A等级的人数是多少?请在图中补全条形统计图.
本次调查的人数为多少人?A等级的人数是多少?请在图中补全条形统计图. 图
图 中,a等于多少?D等级所占的圆心角为多少度?
中,a等于多少?D等级所占的圆心角为多少度?

-
科目: 来源: 题型:
查看答案和解析>>【题目】两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中
 ,
, ,詹姆斯在探究筝形的性质时,得到如下结论:
,詹姆斯在探究筝形的性质时,得到如下结论: ;
; ;
; ≌
≌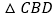 ;
; 四边形ABCD的面积
四边形ABCD的面积 其中正确的结论有
其中正确的结论有


A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AC,BD为对角线,AB=BC=AC=BD,则∠ADC的大小为( )

A. 120°B. 135°C. 145°D. 150°
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算:[(x﹣2y)2+(x﹣2y)(x+2y)﹣2x(2x﹣y)]÷2x
(2)先化简,再求值:2b2+(a+b)(a﹣b)﹣(a﹣b)2,其中a=﹣3,b=
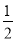 .
.
相关试题

