搜索
【题目】下列说法错误的是（）
A. 两个面积相等的圆一定全等
B. 全等三角形是指形状、大小都相同的三角形
C. 斜边上中线和一条直角边对应相等的两直角三角形全等
D. 底边相等的两个等腰三角形全等
参考答案：
【答案】D
【解析】
根据圆的面积公式可得两个面积相等的圆半径一定也相等，故A说法正确；根据全等三角形的概念可得B说法正确；斜边上中线相等的直角三角形，斜边也相等，再有一条直角边对应相等，故两个直角三角形全等，因此C说法正确．底边相等的两个等腰三角形，腰长不一定相等，故D说法错误；
解：A、两个面积相等的圆一定全等，说法正确；
B、全等三角形是指形状、大小都相同的三角形，说法正确；
C、如图，
在直角三角形ABC和A′B′C′中，
∵BD=B′D′，
∴AC=A′C′,
又AB=A′B′
∴Rt△ABC≌Rt△A′B′C′（HL）
则斜边上中线和一条直角边对应相等的两直角三角形全等，说法正确；
D、底边相等的两个等腰三角形全等，说法错误；
故选：D．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知抛物线y=
x2+bx+c经过△ABC的三个顶点，其中点A（0，1），点B（﹣9，10），AC∥x轴，点P是直线AC下方抛物线上的动点． 
（1）求抛物线的解析式；
（2）过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F，当四边形AECP的面积最大时，求点P的坐标；
（3）当点P为抛物线的顶点时，在直线AC上是否存在点Q，使得以C、P、Q为顶点的三角形与△ABC相似，若存在，求出点Q的坐标，若不存在，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】在矩形ABCD中，AB=3，AD=4，动点Q从点A出发，以每秒1个单位的速度，沿AB向点B移动；同时点P从点B出发，仍以每秒1个单位的速度，沿BC向点C移动，连接QP，QD，PD．若两个点同时运动的时间为x秒（0＜x≤3），解答下列问题：
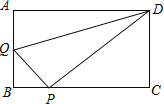
（1）设△QPD的面积为S，用含x的函数关系式表示S；当x为何值时，S有最大值？并求出最小值；
（2）是否存在x的值，使得QP⊥DP？试说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，点O为坐标原点，直线l与抛物线y=mx2+nx相交于A（1，3
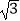），B（4，0）两点．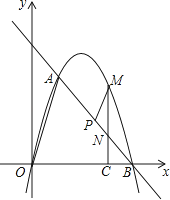 
（1）求出抛物线的解析式；
（2）在坐标轴上是否存在点D，使得△ABD是以线段AB为斜边的直角三角形？若存在，求出点D的坐标；若不存在，说明理由；
（3）点P是线段AB上一动点，（点P不与点A、B重合），过点P作PM∥OA，交第一象限内的抛物线于点M，过点M作MC⊥x轴于点C，交AB于点N，若△BCN、△PMN的面积S△BCN、S△PMN满足S△BCN=2S△PMN ， 求出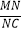
的值，并求出此时点M的坐标． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知△ABC中，a、b、c分别是∠A、∠B、∠C的对边，下列条件不能判断△ABC是直角三角形的是（ ）
A．∠A﹣∠B=∠C
B．∠A：∠B：∠C=3：4：5
C．（b+c）（b﹣c）=a2
D．a=7，b=24，c=25
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在
中
， 
于点
， 
于点
， 
为
边的中点，连接
、
，则下列结论:①
;②
为等边三角形.下面判断正确是( )
A. ①正确 B. ②正确
C. ①②都正确 D. ①②都不正确
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y=x2+bx+c与x轴交于A、B两点，B点坐标为（3，0），与y轴交于点C（0，﹣3）
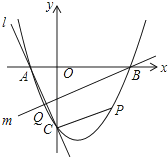
（1）求抛物线的解析式；
（2）点P在抛物线位于第四象限的部分上运动，当四边形ABPC的面积最大时，求点P的坐标和四边形ABPC的最大面积．
（3）直线l经过A、C两点，点Q在抛物线位于y轴左侧的部分上运动，直线m经过点B和点Q，是否存在直线m，使得直线l、m与x轴围成的三角形和直线l、m与y轴围成的三角形相似？若存在，求出直线m的解析式，若不存在，请说明理由．
相关试题
