【题目】已知如图,在平面直角坐标系xOy中,点A、B、C分别为坐标轴上上的三个点,且OA=1,OB=3,OC=4,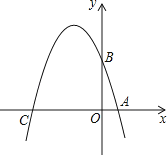
(1)求经过A、B、C三点的抛物线的解析式;
(2)在平面直角坐标系xOy中是否存在一点P,使得以以点A、B、C、P为顶点的四边形为菱形?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)若点M为该抛物线上一动点,在(2)的条件下,请求出当|PM﹣AM|的最大值时点M的坐标,并直接写出|PM﹣AM|的最大值.
参考答案:
【答案】
(1)
解:设抛物线的解析式为y=ax2+bx+c,
∵A(1,0)、B(0,3)、C(﹣4,0),
∴ 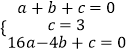 ,
,
解得:a=﹣ ![]() ,b=﹣
,b=﹣ ![]() ,c=3,
,c=3,
∴经过A、B、C三点的抛物线的解析式为y=﹣ ![]() x2﹣
x2﹣ ![]() x+3
x+3
(2)
解:在平面直角坐标系xOy中存在一点P,使得以点A、B、C、P为顶点的四边形为菱形,理由为: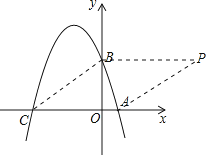
∵OB=3,OC=4,OA=1,
∴BC=AC=5,
当BP平行且等于AC时,四边形ACBP为菱形,
∴BP=AC=5,且点P到x轴的距离等于OB,
∴点P的坐标为(5,3),
当点P在第二、三象限时,以点A、B、C、P为顶点的四边形只能是平行四边形,不是菱形,则当点P的坐标为(5,3)时,以点A、B、C、P为顶点的四边形为菱形.
(3)
解:设直线PA的解析式为y=kx+b(k≠0),
∵A(1,0),P(5,3),
∴ ![]() ,
,
解得:k= ![]() ,b=﹣
,b=﹣ ![]() ,
,
∴直线PA的解析式为y= ![]() x﹣
x﹣ ![]() ,
,
当点M与点P、A不在同一直线上时,根据三角形的三边关系|PM﹣AM|<PA,
当点M与点P、A在同一直线上时,|PM﹣AM|=PA,
∴当点M与点P、A在同一直线上时,|PM﹣AM|的值最大,即点M为直线PA与抛物线的交点,
解方程组 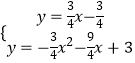 ,得
,得 ![]() 或
或 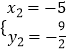 ,
,
∴点M的坐标为(1,0)或(﹣5,﹣ ![]() )时,|PM﹣AM|的值最大,此时|PM﹣AM|的最大值为5.
)时,|PM﹣AM|的值最大,此时|PM﹣AM|的最大值为5.
【解析】(1)设抛物线的解析式为y=ax2+bx+c,把A,B,C三点坐标代入求出a,b,c的值,即可确定出所求抛物线解析式;
(2)在平面直角坐标系xOy中存在一点P,使得以点A、B、C、P为顶点的四边形为菱形,理由为:根据OA,OB,OC的长,利用勾股定理求出BC与AC的长相等,只有当BP与AC平行且相等时,四边形ACBP为菱形,可得出BP的长,由OB的长确定出P的纵坐标,确定出P坐标,当点P在第二、三象限时,以点A、B、C、P为顶点的四边形只能是平行四边形,不是菱形;
(3)利用待定系数法确定出直线PA解析式,当点M与点P、A不在同一直线上时,根据三角形的三边关系|PM﹣AM|<PA,当点M与点P、A在同一直线上时,|PM﹣AM|=PA,
当点M与点P、A在同一直线上时,|PM﹣AM|的值最大,即点M为直线PA与抛物线的交点,联立直线AP与抛物线解析式,求出当|PM﹣AM|的最大值时M坐标,确定出|PM﹣AM|的最大值即可.此题属于二次函数综合题,涉及的知识有:二次函数的性质,待定系数法确定抛物线解析式、一次函数解析式,菱形的判定,以及坐标与图形性质,熟练掌握待定系数法是解本题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D是BC的中点,DE⊥AB于E,DF⊥AC于F,BE=CF.
(1)求证:AD平分∠BAC;
(2)连接EF,求证:AD垂直平分EF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线经过原点O,顶点为A(1,1),且与直线y=x﹣2交于B,C两点.

(1)求抛物线的解析式及点C的坐标;
(2)求证:△ABC是直角三角形;
(3)若点N为x轴上的一个动点,过点N作MN⊥x轴与抛物线交于点M,则是否存在以O,M,N为顶点的三角形与△ABC相似?若存在,请求出点N的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图, AD 为△ ABC 的中线, BE 为△ ABD 的中线.

(1)∠ ABE=15°,∠ BED=55°,求∠ BAD 的度数;
(2)作△ BED 的边 BD 边上的高;
(3)若△ ABC 的面积为 20, BD=2.5,求△ BDE 中 BD 边上的高.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=120°,AB=AC=4,AD⊥BC,BD=2
 ,延长AD到E,使AE=2AD,连接BE.
,延长AD到E,使AE=2AD,连接BE.(1)求证:△ABE为等边三角形;
(2)将一块含60°角的直角三角板PMN如图放置,其中点P与点E重合,且∠NEM=60°,边NE与AB交于点G,边ME与AC交于点F.求证:BG=AF;
(3)在(2)的条件下,求四边形AGEF的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),AB=4cm,AC⊥AB,BD⊥AB,AC=BD=3cm.点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为t(s).
(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,请说明理由,并判断此时线段PC和线段PQ的位置关系;
(2)如图(2),将图(1)中的“AC⊥AB,BD⊥AB”为改“∠CAB=∠DBA=60°”,其他条件不变.设点Q的运动速度为x cm/s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x、t的值;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=
 x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.
x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点. 
(1)求抛物线的解析式;
(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.
相关试题

