【题目】如图,在△ABC中,∠BAC=120°,AB=AC=4,AD⊥BC,BD=2![]() ,延长AD到E,使AE=2AD,连接BE.
,延长AD到E,使AE=2AD,连接BE.
(1)求证:△ABE为等边三角形;
(2)将一块含60°角的直角三角板PMN如图放置,其中点P与点E重合,且∠NEM=60°,边NE与AB交于点G,边ME与AC交于点F.求证:BG=AF;
(3)在(2)的条件下,求四边形AGEF的面积.

参考答案:
【答案】(1)见解析;(2)见解析;(3)4![]()
【解析】试题分析:(1)先证明![]() ,可知AB=2AD,因为AE=2AD,所以AB=AE,从而可知△ABE是等边三角形.
,可知AB=2AD,因为AE=2AD,所以AB=AE,从而可知△ABE是等边三角形.
(2)由(1)可知: ![]() AE=BE,然后求证
AE=BE,然后求证![]() 即可得出BG=AF;
即可得出BG=AF;
(3)由于∴S四边形![]() 故只需求出△ABE的面积即可.
故只需求出△ABE的面积即可.
试题解析:
(1)AB=AC,AD⊥BC,
![]()
![]()
∴AB=2AD,
∵AE=2AD,
∴AB=AE,
![]()
∴△ABE是等边三角形.
(2)∵△ABE是等边三角形,
![]()
AE=BE,
由(1) ![]()
∴∠ABE=∠CAE,
![]()
∴∠NEM∠AEN=∠BEA∠AEN,
∴∠AEF=∠BEG,
在△BEG与△AEF中,
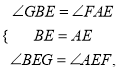
![]()
∴BG=AF;
(3)由(2)可知: ![]()
![]()
∴S四边形![]()
∵△ABE是等边三角形,
∴AE=AB=4,
![]()
∴S四边形![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,用同样规格黑白两色的正方形瓷砖铺设矩形地面,请观察下列图形,并探究和解答下列问题:

(1)设铺设地面所用瓷砖的总块数为y,请写出y与n(表示第n个图形)的关系式;
(2)上述铺设方案,铺一块这样的长方形地面共用了506块瓷砖,求此时n的值;
(3)黑瓷砖每块4元,白瓷砖每块3元,在问题(2)中,共需要花多少钱购买瓷砖?
(4)否存在黑瓷砖与白瓷砖块数相等的情形?请通过计算加以说明
-
科目: 来源: 题型:
查看答案和解析>>【题目】64的立方根是( )
A.4
B.±4
C.8
D.±8 -
科目: 来源: 题型:
查看答案和解析>>【题目】正方形的对称轴的条数为( )
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一元二次方程
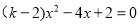 有两个不相等的实数根.
有两个不相等的实数根.(1)求k的取值范围;
(2)如果k是符合条件的最大整数,且一元二次方程
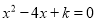 与
与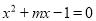 有一个相同的根,求此时
有一个相同的根,求此时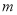 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】中国航空母舰“辽宁号”的满载排水量为67500吨.将数67500用科学记数法表示为( )
A.0.675×105
B.6.75×104
C.67.5×103
D.675×102 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,O为坐标原点,P是反比例函数y=
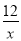 (x>0)图象上任意一点,以P为圆心,PO为半径的圆与坐标轴分别交于点A、B.
(x>0)图象上任意一点,以P为圆心,PO为半径的圆与坐标轴分别交于点A、B.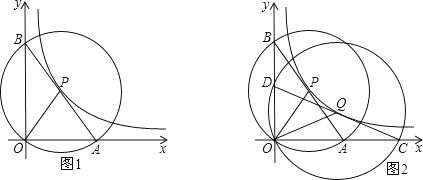
(1)求证:线段AB为⊙P的直径;
(2)求△AOB的面积;
(3)如图2,Q是反比例函数y=
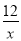 (x>0)图象上异于点P的另一点,以Q为圆心,QO为半径画圆与坐标轴分别交于点C、D.求证:DOOC=BOOA.
(x>0)图象上异于点P的另一点,以Q为圆心,QO为半径画圆与坐标轴分别交于点C、D.求证:DOOC=BOOA.
相关试题

