【题目】如图,已知O为矩形ABCD对角线的交点,过点D作DE∥AC,过点C作CE∥BD,且DE、CE相交于E点. 
(1)求证:四边形OECD是菱形;
(2)若AB=4,AC=8,求菱形OCED的面积.
参考答案:
【答案】
(1)证明:∵CE∥BD,DE∥AC,
∴四边形CODE是平行四边形,
∵四边形ABCD是矩形,
∴AC=BD,OA=OC,OB=OD,
∴OD=OC,
∴四边形CODE是菱形
(2)解:在RT△ABC中,∵∠ABC=90°,AB=4,AC=8,
∴BC= ![]() .
.
∴矩形ABCD的面积=4×4 ![]() =16
=16 ![]() ,
,
∵S△ODC= ![]() S矩形ABCD=4
S矩形ABCD=4 ![]() ,
,
∴四边形OCED的面积=2S△ODC=8 ![]() .
.
【解析】(1)首先由CE∥BD,DE∥AC,可证得四边形CODE是平行四边形,又由四边形ABCD是矩形,根据矩形的性质,易得OC=OD,即可判定四边形CODE是菱形,(2)根据S△ODC= ![]() S矩形ABCD以及四边形OCED的面积=2S△ODC即可解决问题.
S矩形ABCD以及四边形OCED的面积=2S△ODC即可解决问题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】景新中学为了进一步丰富学生的课外阅读,欲增购一些课外书,为此对该校一部分学生进行了一次“你最喜欢的书籍”问卷调查(每人只选一项).根据收集到的数据,绘制成如下统计图(不完整):请根据图中提供的信息,完成下列问题:
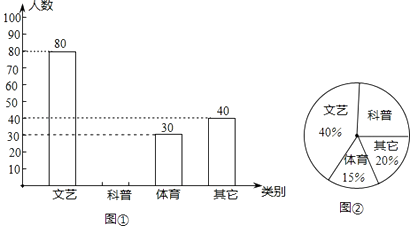
(1)在这次问卷调查中,喜欢“科普书籍”出现的频率为;
(2)在扇形统计图中,喜欢“体育书籍”的所占的圆心角度数为;
(3)如果全校共有学生1500名,请估计该校最喜欢“科普书籍”的学生约有人. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠ABC=90°,点P为射线BC上任意一点(点P与点B不重合),分别以AB、AP为边在∠ABC的内部作等边△ABE和△APQ,连接QE并延长交BP于点F.
(1)如图1,若AB=
 ,点A,E,P恰好在一条直线上时,求EF的长(直接写出结果);
,点A,E,P恰好在一条直线上时,求EF的长(直接写出结果);(2)如图2,当点P为射线BC上任意一点时,求证:BF=EF;
(3)若AB=
 ,设BP=2,求QF的长.
,设BP=2,求QF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,甲、乙两船同时由港口A出发开往海岛B,甲船沿东北方向向海岛B航行,其速度为15海里/小时;乙船速度为20海里/小时,先沿正东方向航行1小时后,到达C港口接旅客,停留半小时后再转向北偏东30°方向开往B岛,其速度仍为20海里/小时.
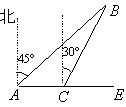
(1)求港口A到海岛B的距离;
(2)B岛建有一座灯塔,在离灯塔方圆5海里内都可以看见灯塔,问甲、乙两船哪一艘先看到灯塔?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为提倡全民健身活动, 某社区准备购买羽毛球和羽毛球拍供社区居民使用, 某体育用品商店羽毛球每盒 10 元, 羽毛球拍每副 40 元 .该商店有两种优惠方案,方案一: 不购买会员卡时, 羽毛球享受 8.5 折优惠, 羽毛球拍购买 5 副(含5 副) 以上才能享受 8.5 折优惠, 5 副以下必须按定价购买;方案二: 每张会员卡 20 元, 办理会员卡时, 全部商品享受 8 折优惠 . 设该社区准备购买羽毛球拍 6 副, 羽毛球
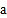 盒, 请回答下列问题:
盒, 请回答下列问题:(1)如果一位体育爱好者按方案一只购买了 4 副羽毛球拍,求他购买时所需要的费用;
(2)用含
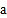 的代数式分别表示该社区按方案一和方案二购买所需要的钱数;
的代数式分别表示该社区按方案一和方案二购买所需要的钱数;(3)①直接写出一个
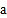 的值, 使方案一比方案二优惠;
的值, 使方案一比方案二优惠;②直接写出一个
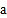 的值, 使方案二比方案一优惠 .
的值, 使方案二比方案一优惠 . -
科目: 来源: 题型:
查看答案和解析>>【题目】2016年2月18日韩国海军海警在朝鲜半岛东部海域实施联合演习,在返回济州岛军事基地途中,韩国海军UH﹣60直升机在距海平面垂直高度为300米的点C处测得济州一小岛的西端点A的俯角为60°,然后沿着平行于AB的方向水平飞行了3500米,在点D测得这小岛的东端点B的俯角为45°,求这个济州小岛东西两端BA的距离(结果精确到1米,参考数据:
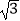 ≈1.732,
≈1.732, 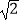 ≈1.414)
≈1.414)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=x+3分别交x,y轴于点D,C,点B在x轴上,OB=OC,过点B作直线m∥CD.点P、Q分别为直线m和直线CD上的动点,且点P在x轴的上方,满足∠POQ=45°
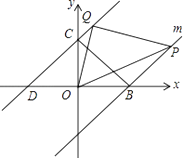
(1)则∠PBO=度;
(2)问:PBCQ的值是否为定值?如果是,请求出该定值;如果不是,请说明理由;
(3)求证:CQ2+PB2=PQ2 .
相关试题

