【题目】反比例函数y= ![]() 的图象经过点A(﹣1,2),则当x>1时,函数值y的取值范围是( )
的图象经过点A(﹣1,2),则当x>1时,函数值y的取值范围是( )
A.y>﹣1
B.﹣1<y<0
C.y<﹣2
D.﹣2<y<0
参考答案:
【答案】D
【解析】解:根据题意, ![]() =2,
=2,
解得k=﹣2,
∴反比例函数解析式为y=﹣ ![]() ,
,
在第四象限内,y值随x的增大而增大,
∴y>﹣ ![]() ,即y>﹣2,
,即y>﹣2,
又∵函数图象在第四象限内,
∴y<0,
∴函数值y的取值范围是﹣2<y<0.
所以答案是:D.
【考点精析】解答此题的关键在于理解一元一次不等式的解法的相关知识,掌握步骤:①去分母;②去括号;③移项;④合并同类项; ⑤系数化为1(特别要注意不等号方向改变的问题),以及对反比例函数的性质的理解,了解性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是等边三角形ABC内部一个动点,∠APB=120°,⊙O是△APB的外接圆.AP,BP的延长线分别交BC,AC于D,E.
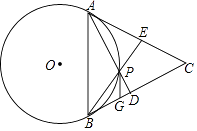
(1)求证:CA,CB是⊙O的切线;
(2)已知AB=6,G在BC上,BG=2,当PG取得最小值时,求PG的长及∠BGP的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】(11·西宁)(本小题满分7分)给出三个整式a2,b2和2ab.
(1)当a=3,b=4时,求a2+b2+2ab的值;
(2)在上面的三个整式中任意选择两个整式进行加法或减法运算,使所得的多项式能够因式分解.请写也你所选的式子及因式分解的过程.
-
科目: 来源: 题型:
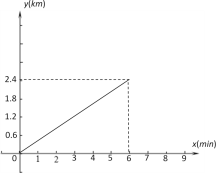
查看答案和解析>>【题目】已知A、B两地相距2.4km,甲骑车匀速从A地前往B地,如图表示甲骑车过程中离A地的路程y(km)与他行驶所用的时间x(min)之间的关系.根据图像解答下列问题:
(1)甲骑车的速度是 km/min;
(2)若在甲出发时,乙在甲前方0.6km处,两人均沿同一路线同时出发匀速前往B地,在第3分钟甲追上了乙,两人到达B地后停止.请在下面同一平面直角坐标系中画出乙离A地的距离y乙(km)与所用时间x(min)的关系的大致图像;
(3)乙在第几分钟到达B地?
(4)两人在整个行驶过程中,何时相距0.2km?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,B在反比例函数
 的图象上,点C,D在反比例函数
的图象上,点C,D在反比例函数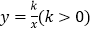 的图象上,AC//BD//y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为
的图象上,AC//BD//y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为 ,则k的值为( )
,则k的值为( )
A. 4 B. 3 C. 2 D.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O为△ABC的外接圆,点E是△ABC的内心,AE的延长线交BC于点F,交⊙O于点D
(1)如图1,求证:BD=ED;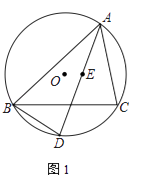
(2)如图2,AD为⊙O的直径.若BC=6,sin∠BAC=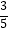 ,求OE的长.
,求OE的长. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正比例函数y=ax与反比例函数
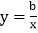 的图象有一个公共点A(1,2).
的图象有一个公共点A(1,2).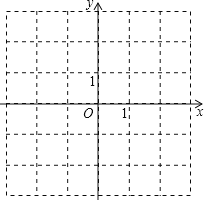
(1)求这两个函数的表达式;
(2)画出草图,根据图象写出正比例函数值大于反比例函数值时x的取值范围.
相关试题

