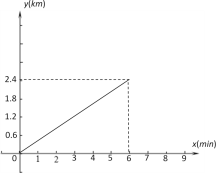
【题目】已知A、B两地相距2.4km,甲骑车匀速从A地前往B地,如图表示甲骑车过程中离A地的路程y(km)与他行驶所用的时间x(min)之间的关系.根据图像解答下列问题:
(1)甲骑车的速度是 km/min;
(2)若在甲出发时,乙在甲前方0.6km处,两人均沿同一路线同时出发匀速前往B地,在第3分钟甲追上了乙,两人到达B地后停止.请在下面同一平面直角坐标系中画出乙离A地的距离y乙(km)与所用时间x(min)的关系的大致图像;
(3)乙在第几分钟到达B地?
(4)两人在整个行驶过程中,何时相距0.2km?
参考答案:
【答案】(1)0.4(2)见解析(3)9分钟 (4)2分钟,4分钟,8分钟.
【解析】
(1)根据速度等于路程除以时间进行解答即可;
(2)根据“在甲出发时,乙在甲前方0.6km处”可知过点(0,0.6),根据“在第3分钟甲追上了乙”可知该图像过横坐标为3的点,过着两点即可画出;
(3)求出y甲=0.4x,把x=3代入y=0.4x,求得y=1.2,再求出 y乙=0.2x+0.6,把y=2.4代入y乙=0.2x+0.6得x=9,所以乙在第9分钟到达B地;
(4)分三种情况,相遇前,相遇后和甲到达后相距0.2km.
解:(1)0.4,
(2)如图:
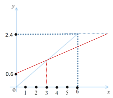
(3)设甲的函数的表达式为y甲=kx,然后把x=6,y=2.4代入求得k=0.4,所以函数表达式为y甲=0.4x,把x=3代入y=0.4x,求得y=1.2,
设乙的函数表达式为y乙=kx+b,然后把x=0,y=0.6;x=3,y=1.2分别代入
求得k=0.2,b=0.6,所以函数表达式为y乙=0.2x+0.6,
把y=2.4代入y乙=0.2x+0.6得x=9,
所以乙在第9分钟到达B地.
(4)①相遇前是y乙-y甲=0.2即0.2x+0.6-0.4x=0.2,解得x=2,
所以在第2分钟两人相距0.2km;
②相遇后是y甲-y乙=0.2即0.4x-(0.2x+0.6)=0.2,解得x=4,
所以在第4分钟两人相距0.2km.
③把y=2.2代入y乙=0.2x+0.6得x=8,
所以第8分钟时两人相距0.2km.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)5a2b÷
 ×2ab2;
×2ab2;(2)[(x+2y)2-(x+y)(x-y)-5y2]÷2x;
(3)(-3.6×1010)÷(-2×102)2;
(4)(2a-b+3)(2a-3+b).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是等边三角形ABC内部一个动点,∠APB=120°,⊙O是△APB的外接圆.AP,BP的延长线分别交BC,AC于D,E.
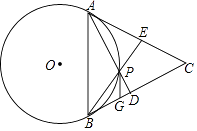
(1)求证:CA,CB是⊙O的切线;
(2)已知AB=6,G在BC上,BG=2,当PG取得最小值时,求PG的长及∠BGP的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】(11·西宁)(本小题满分7分)给出三个整式a2,b2和2ab.
(1)当a=3,b=4时,求a2+b2+2ab的值;
(2)在上面的三个整式中任意选择两个整式进行加法或减法运算,使所得的多项式能够因式分解.请写也你所选的式子及因式分解的过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】反比例函数y=
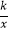 的图象经过点A(﹣1,2),则当x>1时,函数值y的取值范围是( )
的图象经过点A(﹣1,2),则当x>1时,函数值y的取值范围是( )
A.y>﹣1
B.﹣1<y<0
C.y<﹣2
D.﹣2<y<0 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,B在反比例函数
 的图象上,点C,D在反比例函数
的图象上,点C,D在反比例函数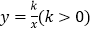 的图象上,AC//BD//y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为
的图象上,AC//BD//y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为 ,则k的值为( )
,则k的值为( )
A. 4 B. 3 C. 2 D.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O为△ABC的外接圆,点E是△ABC的内心,AE的延长线交BC于点F,交⊙O于点D
(1)如图1,求证:BD=ED;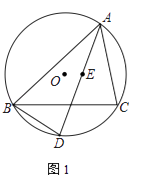
(2)如图2,AD为⊙O的直径.若BC=6,sin∠BAC=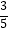 ,求OE的长.
,求OE的长. 
相关试题

