【题目】如图,点P是等边三角形ABC内部一个动点,∠APB=120°,⊙O是△APB的外接圆.AP,BP的延长线分别交BC,AC于D,E. 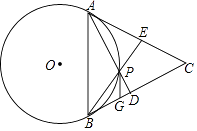
(1)求证:CA,CB是⊙O的切线;
(2)已知AB=6,G在BC上,BG=2,当PG取得最小值时,求PG的长及∠BGP的度数.
参考答案:
【答案】
(1)证明:连接OA,OB,在⊙O上取一点M,连接AM,BM,
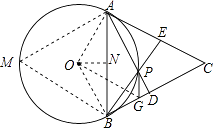
∴四边形APBM是圆内接四边形,
∴∠M=180°﹣∠APB=60°,
∵∠AOB=2∠M=120°,
∵OA=OB,
∴∠OAB=∠OBA=30°,
∴∠BAC=60°,
∴∠OBC=90°,
∴CB是⊙O的切线;
同理CA是⊙O的切线
(2)作ON⊥AB于N,连接OG,

当O,P,G在一条直线上时,PG最小,
∵AB=6,
∴BN=3,
∴OB=2 ![]() ,
,
∵∠OBG=90°,BG=2,tan∠OGB= ![]() ,
,
∴∠OGB=60°,OG=4,
∴PG=4﹣2 ![]() ,
,
此时,∠BGP=60°.
【解析】(1)连接OA,OB,在⊙O上取一点M,连接AM,BM,根据圆内接四边形的性质得到∠M=180°﹣∠APB=60°,根据圆周角定理得到∠AOB=2∠M=120°,求得∠BAC=60°,于是得到结论;(2)作ON⊥AB于N,连接OG,当O,P,G在一条直线上时,PG最小,解直角三角形即可得到结论.
【考点精析】本题主要考查了等边三角形的性质和三角形的外接圆与外心的相关知识点,需要掌握等边三角形的三个角都相等并且每个角都是60°;过三角形的三个顶点的圆叫做三角形的外接圆,其圆心叫做三角形的外心才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣2x+7与x轴、y轴分别相交于点C、B,与直线y=
 x相交于点A.
x相交于点A.(1)求A点坐标;
(2)求△OAC的面积;
(3)如果在y轴上存在一点P,使△OAP是以OA为底边的等腰三角形,求P点坐标;
(4)在直线y=﹣2x+7上是否存在点Q,使△OAQ的面积等于6?若存在,请求出Q点的坐标,若不存在,请说明理由.

-
科目: 来源: 题型:
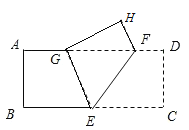
查看答案和解析>>【题目】如图,把长方形纸片ABCD沿EF折叠后,使得点D落在点H的位置上,点C恰好落在边AD上的点G处,连接EG.
(1)△GEF是等腰三角形吗?请说明理由;
(2)若CD=4,GD=8,求HF的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)5a2b÷
 ×2ab2;
×2ab2;(2)[(x+2y)2-(x+y)(x-y)-5y2]÷2x;
(3)(-3.6×1010)÷(-2×102)2;
(4)(2a-b+3)(2a-3+b).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(11·西宁)(本小题满分7分)给出三个整式a2,b2和2ab.
(1)当a=3,b=4时,求a2+b2+2ab的值;
(2)在上面的三个整式中任意选择两个整式进行加法或减法运算,使所得的多项式能够因式分解.请写也你所选的式子及因式分解的过程.
-
科目: 来源: 题型:
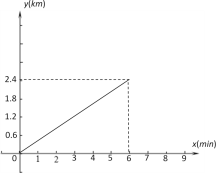
查看答案和解析>>【题目】已知A、B两地相距2.4km,甲骑车匀速从A地前往B地,如图表示甲骑车过程中离A地的路程y(km)与他行驶所用的时间x(min)之间的关系.根据图像解答下列问题:
(1)甲骑车的速度是 km/min;
(2)若在甲出发时,乙在甲前方0.6km处,两人均沿同一路线同时出发匀速前往B地,在第3分钟甲追上了乙,两人到达B地后停止.请在下面同一平面直角坐标系中画出乙离A地的距离y乙(km)与所用时间x(min)的关系的大致图像;
(3)乙在第几分钟到达B地?
(4)两人在整个行驶过程中,何时相距0.2km?
-
科目: 来源: 题型:
查看答案和解析>>【题目】反比例函数y=
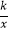 的图象经过点A(﹣1,2),则当x>1时,函数值y的取值范围是( )
的图象经过点A(﹣1,2),则当x>1时,函数值y的取值范围是( )
A.y>﹣1
B.﹣1<y<0
C.y<﹣2
D.﹣2<y<0
相关试题

