【题目】如图,在平面直角坐标系xOy中,平行四边形OABC的顶点A,B的坐标分别为(6,0),(7,3),将平行四边形OABC绕点O逆时针方向旋转得到平行四边形OA′B′C′,当点C′落在BC的延长线上时,线段OA′交BC于点E,则线段C′E的长度为 . 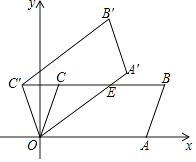
参考答案:
【答案】5
【解析】解:∵OC=OC′,CC′⊥y轴,A,B的坐标分别为(6,0),(7,3),
∴点C到y轴的距离:7﹣6=1.
∴O′C=O′C′=1,O点到CC′的距离是3,
∴OC=OC′= ![]() ,S△OCC′=
,S△OCC′= ![]() ×2×3=3.
×2×3=3.
如图,过点C作CD⊥OC′于点D,则 ![]() OC′CD=3,
OC′CD=3,
∴CD= ![]() ,sin∠COC′=
,sin∠COC′= ![]() =
= ![]() ,tan∠COC′=
,tan∠COC′= ![]() .
.
∵∠COC′+∠COE=∠AOE+∠COE,
∴∠COC′=∠AOE,
∴tan∠AOE=tan∠COC′= ![]() .
.
如图,过E作x轴的垂线,交x轴于点F,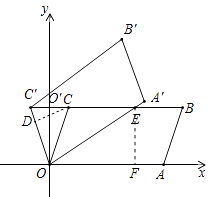
则EF=OO'=3.
∵tan∠AOE= ![]() ,
,
∴OF= ![]() =4,
=4,
∵OF=O′E=4,
∴C′E=O′E+O′C′=4+1=5.
故答案为:5.
过点C作CD⊥OC′于点D.利用旋转的性质和面积法求得CD的长,然后通过解直角三角形推知:tan∠COC′= ![]() .结合图形和旋转的性质得到∠COC′=∠AOE,自点E向x轴引垂线,交x轴于点F,则EF=3.利用等角的正切值相等tan∠AOE=tan∠COC′=
.结合图形和旋转的性质得到∠COC′=∠AOE,自点E向x轴引垂线,交x轴于点F,则EF=3.利用等角的正切值相等tan∠AOE=tan∠COC′= ![]() =
= ![]() ,进而求得OF的长度,则C′E=O′E+O′C=4+1=5.
,进而求得OF的长度,则C′E=O′E+O′C=4+1=5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一个转盘,转盘被分成4个相同的扇形,颜色分为红、绿、黄三种,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形),求下列事件的概率:
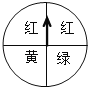
(1)指针指向绿色;
(2)指针指向红色或黄色;
(3)指针不指向红色.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=5,OC=4.

(1)在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,则D点的坐标;E点的坐标 .
(2)如图②,若AE上有一动点P(不与A、E重合)自A点沿AE方向向E点匀速运动,运动的速度为每秒1个单位长度,设运动的时间为t秒(0<t<5),过P点作ED的平行线交AD于点M,过点M作AE的平行线交DE于点N.求四边形PMNE的面积S与时间t之间的函数关系式;t取何值时,S有最大值,最大值是多少?
(3)在(2)的条件下,当t为何值时,以A、M、E为顶点的三角形为等腰三角形,并求出相应时刻点M的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两人分别驾车从
 同时出发,沿同一条线路相向而行,甲从
同时出发,沿同一条线路相向而行,甲从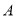 地以速度52km/h匀速去
地以速度52km/h匀速去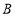 地,乙开始以速度
地,乙开始以速度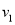 km/h匀速行驶,中途速度改为
km/h匀速行驶,中途速度改为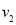 km/h匀速行驶,到
km/h匀速行驶,到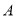 恰好用时
恰好用时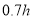 ,两人距离
,两人距离 地的路程与各自离开出发地的时间之间的图象如图所示.求:
地的路程与各自离开出发地的时间之间的图象如图所示.求:(1)
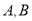 两地之间的路程为多少
两地之间的路程为多少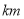 及乙开始的速度
及乙开始的速度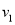 ;
;(2)当两人相距
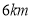 时,求
时,求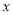 的值.
的值.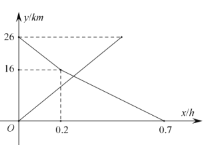
-
科目: 来源: 题型:
查看答案和解析>>【题目】小颖和小红两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)试验,她们共做了60次试验,试验的结果如下:
朝上的点数
1
2
3
4
5
6
出现的次数
7
9
6
8
20
10
(1)计算“3点朝上”的频率和“5点朝上”的频率.
(2)小颖说:“根据上述试验,一次试验中出现5点朝上的概率最大”;小红说:“如果投掷600次,那么出现6点朝上的次数正好是100次”.小颖和小红的说法正确吗?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=
 x+2交x轴于点A,交y轴于点B,点P(x,y)是线段AB上一动点(与A,B不重合),△PAO的面积为S,求S与x的函数关系式,并写出自变量的取值范围.
x+2交x轴于点A,交y轴于点B,点P(x,y)是线段AB上一动点(与A,B不重合),△PAO的面积为S,求S与x的函数关系式,并写出自变量的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】重庆八中七年级 16 班同学为了解2019年某小区家庭月均用水情况,进行了一次社会实践活动.他们随机调查了该小区部分家庭,并将调查数据进行如下整理,
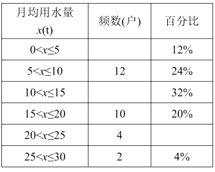
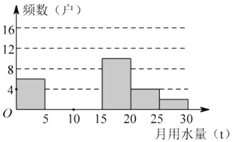
请解答以下问题:
(1)把上面的频数分布表和频数分布直方图补充完整;
(2)若重庆市准备实施的阶梯水价中,计划对月用水量不超过 15 吨的家庭实施水价下浮政策.为此,该班同学随机从这些用户中抽取一户进行采访.则抽到的采访用户属于月用水量不超过 5 吨的概率是多少?
相关试题

