【题目】如图①,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=5,OC=4.
(1)在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,则D点的坐标;E点的坐标 .
(2)如图②,若AE上有一动点P(不与A、E重合)自A点沿AE方向向E点匀速运动,运动的速度为每秒1个单位长度,设运动的时间为t秒(0<t<5),过P点作ED的平行线交AD于点M,过点M作AE的平行线交DE于点N.求四边形PMNE的面积S与时间t之间的函数关系式;t取何值时,S有最大值,最大值是多少?
(3)在(2)的条件下,当t为何值时,以A、M、E为顶点的三角形为等腰三角形,并求出相应时刻点M的坐标.
参考答案:
【答案】
(1)(0,2.5),(2,4)
(2)解:∵PM∥ED,
∴△APM∽△AED.
∴PM:ED=AP:AE,
∴PM= ![]() ,
,
又∵AP=t,ED=2.5,AE=5,
∴PM= ![]() =
= ![]() t,
t,
∵PM∥DE,MN∥EP,
∴四边形NMPE为平行四边形.
又∵∠DEA=90°,
∴四边形PMNE为矩形.
∴S矩形PMNE=PMPE= ![]() t(5﹣t)=﹣
t(5﹣t)=﹣ ![]() t2+
t2+ ![]() t.
t.
∴S矩形PMNE=﹣ ![]() (t﹣
(t﹣ ![]() )2+
)2+ ![]() ,
,
又∵0< ![]() <5.
<5.
∴当t= ![]() 时,S矩形PMNE有最大值
时,S矩形PMNE有最大值 ![]() .
.
(3)解:(Ⅰ)若以AE为等腰三角形的底,则ME=MA(如图①)
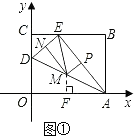
在Rt△AED中,ME=MA,
∵PM⊥AE,
∴P为AE的中点,
∴t=AP= ![]() AE=2.5.
AE=2.5.
又∵PM∥ED,
∴M为AD的中点.
过点M作MF⊥OA,垂足为F,则MF是△OAD的中位线,
∴MF= ![]() OD=
OD= ![]() ,OF=
,OF= ![]() OA=2.5,
OA=2.5,
∴当t=2.5时,(0<2.5<5),△AME为等腰三角形.
此时M点坐标为(2.5,1.25).
(Ⅱ)若以AE为等腰三角形的腰,则AM=AE=5(如图②)
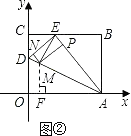
在Rt△AOD中,AD= ![]() =
= ![]() .
.
过点M作MF⊥OA,垂足为F.
∵PM∥ED,
∴△APM∽△AED.
∴AP:AE=AM:AD.
∴t=AP= ![]() =2
=2 ![]() .
.
∴PM= ![]() t=
t= ![]() .
.
∴MF=MP= ![]() ,OF=OA﹣AF=OA﹣AP=5﹣2
,OF=OA﹣AF=OA﹣AP=5﹣2 ![]() ,
,
∴当t=2 ![]() 时,(0<2
时,(0<2 ![]() <5),此时M点坐标为(5﹣2
<5),此时M点坐标为(5﹣2 ![]() ,
, ![]() ).
).
(Ⅲ)根据图形可知EM=EA的情况不成立.
综合综上所述,当t=2.5或t=2 ![]() 时,以A,M,E为顶点的三角形为等腰三角形,相应M点的坐标为(
时,以A,M,E为顶点的三角形为等腰三角形,相应M点的坐标为( ![]() ,
, ![]() )或(5﹣2
)或(5﹣2 ![]() ,
, ![]() ).
).
【解析】解:(1)依题意可知,折痕AD是四边形OAED的对称轴,
∵在Rt△ABE中,AE=AO=5,AB=4,BE= ![]() =3.
=3.
∴CE=2.
∴E点坐标为(2,4).
在Rt△DCE中,DC2+CE2=DE2,
又∵DE=OD.
∴(4﹣OD)2+22=OD2.
解得:OD=2.5.
∴D点坐标为(0,2.5).
所以答案是:(0,2.5),(2,4);
【考点精析】本题主要考查了二次函数的最值和勾股定理的概念的相关知识点,需要掌握如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求,商家又用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.
(1)该商家购进的第一批衬衫是多少件?
(2)若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完后利润不低于25%(不考虑其他因素),那么每件衬衫的标价至少是多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=﹣x+b与反比例函数y=
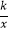 (k≠0)的图象相交于A(﹣1,4)、B(4,﹣1)两点,直线l⊥x轴于点E(﹣4,0),与反比例函数和一次函数的图象分别相交于点C、D,连接AC、BC
(k≠0)的图象相交于A(﹣1,4)、B(4,﹣1)两点,直线l⊥x轴于点E(﹣4,0),与反比例函数和一次函数的图象分别相交于点C、D,连接AC、BC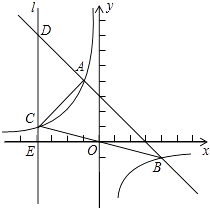
(1)求出b和k;
(2)求证:△ACD是等腰直角三角形;
(3)在y轴上是否存在点P,使S△PBC=S△ABC?若存在,请求出P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一个转盘,转盘被分成4个相同的扇形,颜色分为红、绿、黄三种,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形),求下列事件的概率:
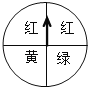
(1)指针指向绿色;
(2)指针指向红色或黄色;
(3)指针不指向红色.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两人分别驾车从
 同时出发,沿同一条线路相向而行,甲从
同时出发,沿同一条线路相向而行,甲从 地以速度52km/h匀速去
地以速度52km/h匀速去 地,乙开始以速度
地,乙开始以速度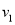 km/h匀速行驶,中途速度改为
km/h匀速行驶,中途速度改为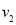 km/h匀速行驶,到
km/h匀速行驶,到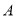 恰好用时
恰好用时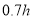 ,两人距离
,两人距离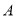 地的路程与各自离开出发地的时间之间的图象如图所示.求:
地的路程与各自离开出发地的时间之间的图象如图所示.求:(1)
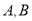 两地之间的路程为多少
两地之间的路程为多少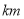 及乙开始的速度
及乙开始的速度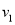 ;
;(2)当两人相距
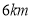 时,求
时,求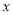 的值.
的值.
-
科目: 来源: 题型:
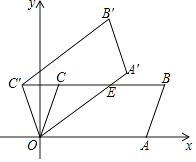
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,平行四边形OABC的顶点A,B的坐标分别为(6,0),(7,3),将平行四边形OABC绕点O逆时针方向旋转得到平行四边形OA′B′C′,当点C′落在BC的延长线上时,线段OA′交BC于点E,则线段C′E的长度为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】小颖和小红两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)试验,她们共做了60次试验,试验的结果如下:
朝上的点数
1
2
3
4
5
6
出现的次数
7
9
6
8
20
10
(1)计算“3点朝上”的频率和“5点朝上”的频率.
(2)小颖说:“根据上述试验,一次试验中出现5点朝上的概率最大”;小红说:“如果投掷600次,那么出现6点朝上的次数正好是100次”.小颖和小红的说法正确吗?为什么?
相关试题

