【题目】如图,在平面直角坐标系xOy中,函数y=-x的图象l是第二、四象限的角平分线.
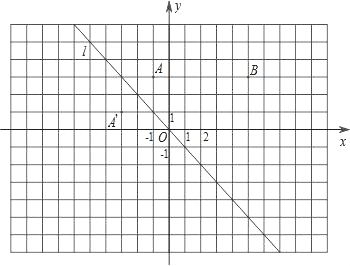
(1)实验与探究:由图观察易知A(-1,3)关于直线l的对称点A′的坐标为(-3,1),请你写出点B(5,3)关于直线l的对称点B′的坐标为 ;
(2)归纳与发现:结合图形,自己选点再试一试,通过观察点的坐标,你会发现:坐标平面内任一点P(m,n)关于第二、四象限的角平分线l的对称点P′的坐标为 ;
(3)运用与拓广:
①已知两点C(6,0),D(2,4),试在直线l上确定一点P,使点P到C,D两点的距离之和最小,在图中画出点P的位置,保留作图痕迹,并求出点P的坐标.
②在①的条件下,试求出PC+PD的最小值.
参考答案:
【答案】(1)(-3,-5);(2)(-n,-m);(3)①作图见解析;P(1,-1);②![]() .
.
【解析】
试题分析:(1)观察图形得出点B(5,3)关于直线l的对称点B′的坐标即可;
(2)归纳总结得到一般性规律,写出P(m,n)关于第二、四象限的角平分线l的对称点P′的坐标即可;
(3)①如图,作点C关于直线 l 的对称点C′,连接C′D,交l于点P,连接CP,由作图可知,PC=PC′,进而得到PC+PD=C′D,求出此时P坐标即可;②利用勾股定理求出PC+PD的最小值即可.
试题解析:(1)根据题意得:B′(-3,-5);
(2)根据题意得:P′(-n,-m);
(3)①如图,作点C关于直线 l 的对称点C′,连接C′D,交l于点P,连接CP,
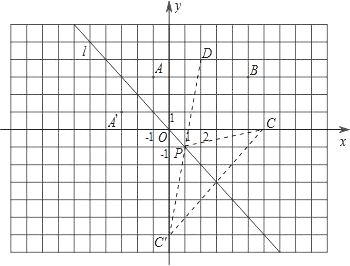
由作图可知,PC=PC′,
∴PC+PD=PC′+PD=C′D,
∴点P为所求,
∵C(6,0),
∴C′(0,-6).
设直线C′D的解析式为y=kx-6,
∵D(2,4),
∴k=5,
∴直线C′D的解析式为y=5x-6,
由![]() 得
得![]() ,
,
∴P(1,-1);
②PC+PD=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】指出下列命题的条件和结论.
(1)两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行;
(2)如果∠1=∠2,∠2=∠3,那么∠1=∠3;
(3)锐角小于它的余角;
(4)如果a+c=b+c,那么a=b.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若等腰直角三角形斜边的平方为2,求它的直角边长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】写出一个3到4之间的无理数 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=x2+bx+c与y轴交于点C,与x轴交于点A、B,且AB=2,抛物线的对称轴为直线x=2;
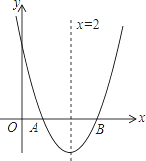
(1)求抛物线的函数表达式;
(2)如果抛物线的对称轴上存在一点P,使得△APC周长的值最小,求此时P点坐标及△APC周长;
(3)设D为抛物线上一点,E为对称轴上一点,若以点A、B、D、E为顶点的四边形是平行四边形,求点D的坐标.(直接写出结果)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的半径为4,B是⊙O外一点,连接OB,且OB=6,延长BO交⊙O于点A,点D为⊙O上一点,过点A作直线BD的垂线,垂足为C,AD平分∠BAC.
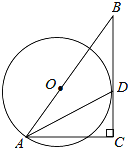
(1)求证:BC是⊙O的切线;
(2)求AC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知ABCD中,AE⊥BC于点E,以点B为中心,取旋转角等于∠ABC,把△BAE顺时针旋转,得到△BA′E′,连接DA′.若∠ADC=60°,∠ADA′=50°,则∠DA′E′的大小为( )

A.130° B.150° C.160° D.170°
相关试题

