搜索
【题目】如图，已知ABCD中，AE⊥BC于点E，以点B为中心，取旋转角等于∠ABC，把△BAE顺时针旋转，得到△BA′E′，连接DA′．若∠ADC=60°，∠ADA′=50°，则∠DA′E′的大小为（ ）
A．130° B．150° C．160° D．170°
参考答案：
【答案】C
【解析】
试题分析：根据平行四边形对角相等、邻角互补，得∠ABC=60°，∠DCB=120°，再由∠A′DC=10°，可运用三角形外角求出∠DA′B=130°，再根据旋转的性质得到∠BA′E′=∠BAE=30°，从而得到答案．
解：∵四边形ABCD是平行四边形，∠ADC=60°，
∴∠ABC=60°，∠DCB=120°，
∵∠ADA′=50°，
∴∠A′DC=10°，
∴∠DA′B=130°，
∵AE⊥BC于点E，
∴∠BAE=30°，
∵△BAE顺时针旋转，得到△BA′E′，
∴∠BA′E′=∠BAE=30°，
∴∠DA′E′=∠DA′B+∠BA′E′=160°．
故选：C．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系xOy中，函数y=-x的图象l是第二、四象限的角平分线．
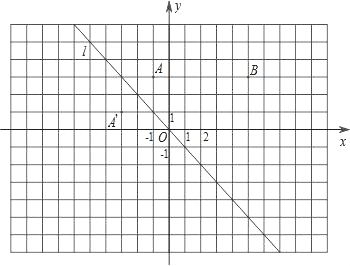
（1）实验与探究：由图观察易知A（-1，3）关于直线l的对称点A′的坐标为（-3，1），请你写出点B（5，3）关于直线l的对称点B′的坐标为 ；
（2）归纳与发现：结合图形，自己选点再试一试，通过观察点的坐标，你会发现：坐标平面内任一点P（m，n）关于第二、四象限的角平分线l的对称点P′的坐标为 ；
（3）运用与拓广：
①已知两点C（6，0），D（2，4），试在直线l上确定一点P，使点P到C，D两点的距离之和最小，在图中画出点P的位置，保留作图痕迹，并求出点P的坐标．
②在①的条件下，试求出PC+PD的最小值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知抛物线y=x2+bx+c与y轴交于点C，与x轴交于点A、B，且AB=2，抛物线的对称轴为直线x=2；
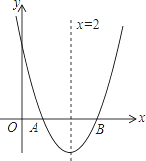
（1）求抛物线的函数表达式；
（2）如果抛物线的对称轴上存在一点P，使得△APC周长的值最小，求此时P点坐标及△APC周长；
（3）设D为抛物线上一点，E为对称轴上一点，若以点A、B、D、E为顶点的四边形是平行四边形，求点D的坐标．（直接写出结果）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，⊙O的半径为4，B是⊙O外一点，连接OB，且OB=6，延长BO交⊙O于点A，点D为⊙O上一点，过点A作直线BD的垂线，垂足为C，AD平分∠BAC．
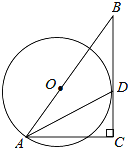
（1）求证：BC是⊙O的切线；
（2）求AC的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，点O是坐标原点，四边形ABCO是菱形，点A的坐标为（-3，4），点C在x轴的正半轴上，直线AC交y轴于点M，AB边交y轴于点H，连接BM．
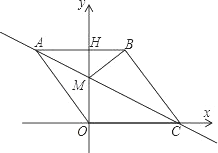
（1）求直线AC的解析式；
（2）动点P从点A出发，沿折线ABC的方向以2个单位/秒的速度向终点C匀速运动，设△PMB的面积为S，点P的运动时间为t秒，求S与t之间的函数关系式（要求写出自变量t的取值范围）；
（3）动点P从点A出发，沿线段AB方向以2个单位/秒的速度向终点B匀速运动，当∠MPB与∠BCO互为余角时，试确定t的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，D、E分别是AB、AC的中点，过点E作EF∥AB，交BC于点F．
（1）求证：四边形DBFE是平行四边形；
（2）当△ABC满足什么条件时，四边形DBFE是菱形？为什么？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，Rt△AOB的一条直角边OB在x轴上，双曲线y=
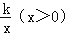经过斜边OA的中点C，与另一直角边交于点D．若S△OCD=9，则S△OBD的值为 ．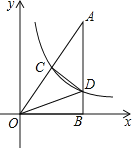
相关试题
