【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 在
在![]() 内,
内,![]() ,
,![]() ,点
,点![]() 在
在![]() 外,
外,![]() ,
,![]() .
.
(1)求![]() 的度数;
的度数;
(2)判断![]() 的形状并加以证明;
的形状并加以证明;
(3)连接![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.

参考答案:
【答案】(1) 150°;(2) △ABE是等边三角形,理由见解析;(3)4
【解析】
(1)首先证明△DBC是等边三角形,推出∠BDC=60°,再证明△ADB≌△ADC,推出∠ADB=∠ADC即可解决问题.
(2)结论:△ABE是等边三角形.只要证明△ABD≌△EBC即可.
(3)首先证明△DEC是含有30度角的直角三角形,求出EC的长,理由全等三角形的性质即可解决问题.
(1)解:∵BD=BC,∠DBC=60°,
∴△DBC是等边三角形,∴DB=DC,∠BDC=∠DBC=∠DCB=60°,
在△ADB和△ADC中,
 ,
,
∴△ADB≌△ADC,∴∠ADB=∠ADC,∴∠ADB=![]() (360°﹣60°)=150°.
(360°﹣60°)=150°.
(2)解:结论:△ABE是等边三角形.
理由:∵∠ABE=∠DBC=60°,∴∠ABD=∠CBE,
在△ABD和△EBC中,
 ,
,
∴△ABD≌△EBC,∴AB=BE,∵∠ABE=60°,∴△ABE是等边三角形.
(3)解:连接DE.

∵∠BCE=150°,∠DCB=60°,∴∠DCE=90°,∵∠EDB=90°,∠BDC=60°,
∴∠EDC=30°,∴EC=![]() DE=4,∵△ABD≌△EBC,∴AD=EC=4.
DE=4,∵△ABD≌△EBC,∴AD=EC=4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请你根据如图所示的阿宝与仙鹤的对话,解答下列问题:
(1)仙鹤为什么说多边形内角和的度数不可能是
 ;
;(2)若图中仙鹤所提到的外角的度数为
 ,请分别求仙鹤所画的多边形的内角和的度数与边数.
,请分别求仙鹤所画的多边形的内角和的度数与边数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=x2+bx+c经过A(﹣1,0)、B(3,0)两点.

(1)求抛物线的解析式和顶点坐标;
(2)当0<x<3时,求y的取值范围;
(3)点P为抛物线上一点,若S△PAB=10,求出此时点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课的变化而变化.开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指数y随时间x(分钟)的变化规律如下图所示(其中AB、BC分别为线段,CD为双曲线的一部分):

(1)求出线段AB,曲线CD的解析式,并写出自变量的取值范围;
(2)开始上课后第五分钟时与第三十分钟时相比较,何时学生的注意力更集中?
(3)一道数学竞赛题,需要讲19分钟,为了效果较好,要求学生的注意力指数最低达到36,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目? -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,点
中,点 ,点
,点 是
是 轴上两点,其中
轴上两点,其中 ,点
,点 都在
都在 轴上,
轴上, 在射线
在射线 上(不与点
上(不与点 重合),
重合), ,连结
,连结 .
.(1)求
 、
、 的坐标;
的坐标;(2)如图
 ,若
,若 在
在 轴正半轴,
轴正半轴, 在线段
在线段 上,当
上,当 时,求证:
时,求证: 为等边三角形;(提示:连结
为等边三角形;(提示:连结 )
)(3)当
 时,在图
时,在图 中画出示意图,设
中画出示意图,设 ,若
,若 ,求
,求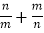 的值.
的值.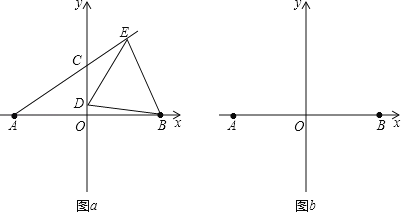
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC为边长为6的等边三角形,D,E分别在边BC,AC上,且CD=CE=x,连接DE并延长至点F,使EF=AE,连接AF,CF.

(1)求证:△AEF为等边三角形;
(2)求证:四边形ABDF是平行四边形;
(3)记△CEF的面积为S,
①求S与x的函数关系式;
②当S有最大值时,判断CF与BC的位置关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】不等式组
 的解在数轴上表示为( )
的解在数轴上表示为( )
A.
B.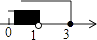
C.
D.
相关试题

