【题目】如图,已知抛物线y=x2+bx+c经过A(﹣1,0)、B(3,0)两点.
(1)求抛物线的解析式和顶点坐标;
(2)当0<x<3时,求y的取值范围;
(3)点P为抛物线上一点,若S△PAB=10,求出此时点P的坐标.
参考答案:
【答案】
(1)解:把A(﹣1,0)、B(3,0)分别代入y=x2+bx+c中,
得: ![]() ,解得:
,解得: ![]() ,
,
∴抛物线的解析式为y=x2﹣2x﹣3.
∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴顶点坐标为(1,﹣4)
(2)解:由图可得当0<x<3时,﹣4≤y<0
(3)解:∵A(﹣1,0)、B(3,0),
∴AB=4.
设P(x,y),则S△PAB= ![]() AB|y|=2|y|=10,
AB|y|=2|y|=10,
∴|y|=5,
∴y=±5.
①当y=5时,x2﹣2x﹣3=5,解得:x1=﹣2,x2=4,
此时P点坐标为(﹣2,5)或(4,5);
②当y=﹣5时,x2﹣2x﹣3=﹣5,方程无解;
综上所述,P点坐标为(﹣2,5)或(4,5).
【解析】(1)方法1:将A、B两点坐标代入函数解析式建立二元一次方程组求出b、c的值,方法2:因为A(﹣1,0)、B(3,0)所以可设函数解析式为y=a(x-3)(x+1),由a=1,可求出函数解析式,再利用配方法或代入顶点坐标就可以求出抛物线的顶点坐标;(2)结合图像以及点A、B的坐标即可得出结论;(3)设点P(x,y),根据三角形的面积公式以及S△PAB=10,即可求出y的值,将y=±5分别代入函数解析式就可以求出点P的坐标。
-
科目: 来源: 题型:
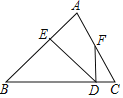
查看答案和解析>>【题目】如图所示,
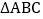 中,
中,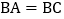 ,点
,点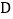 为
为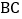 上一点,
上一点,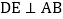 交
交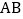 于点
于点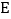 ,
, 交
交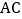 于点
于点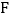 .
.(1)若
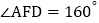 ,则
,则 °;
°; (2)若点
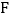 是
是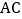 的中点,求证:
的中点,求证: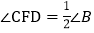 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1=∠3,CD∥EF,试说明∠1=∠4.请将过程填写完整.

解:∵∠1=∠3,
又∠2=∠3(_______),
∴∠1=____,
∴______∥______(_______),
又∵CD∥EF,
∴AB∥_____,
∴∠1=∠4(两直线平行,同位角相等).
-
科目: 来源: 题型:
查看答案和解析>>【题目】请你根据如图所示的阿宝与仙鹤的对话,解答下列问题:
(1)仙鹤为什么说多边形内角和的度数不可能是
 ;
;(2)若图中仙鹤所提到的外角的度数为
 ,请分别求仙鹤所画的多边形的内角和的度数与边数.
,请分别求仙鹤所画的多边形的内角和的度数与边数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课的变化而变化.开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指数y随时间x(分钟)的变化规律如下图所示(其中AB、BC分别为线段,CD为双曲线的一部分):

(1)求出线段AB,曲线CD的解析式,并写出自变量的取值范围;
(2)开始上课后第五分钟时与第三十分钟时相比较,何时学生的注意力更集中?
(3)一道数学竞赛题,需要讲19分钟,为了效果较好,要求学生的注意力指数最低达到36,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中,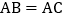 ,点
,点 在
在 内,
内, ,
, ,点
,点 在
在 外,
外, ,
, .
.(1)求
 的度数;
的度数;(2)判断
 的形状并加以证明;
的形状并加以证明;(3)连接
 ,若
,若 ,
, ,求
,求 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,点
中,点 ,点
,点 是
是 轴上两点,其中
轴上两点,其中 ,点
,点 都在
都在 轴上,
轴上,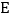 在射线
在射线 上(不与点
上(不与点 重合),
重合), ,连结
,连结 .
.(1)求
 、
、 的坐标;
的坐标;(2)如图
 ,若
,若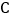 在
在 轴正半轴,
轴正半轴, 在线段
在线段 上,当
上,当 时,求证:
时,求证: 为等边三角形;(提示:连结
为等边三角形;(提示:连结 )
)(3)当
 时,在图
时,在图 中画出示意图,设
中画出示意图,设 ,若
,若 ,求
,求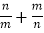 的值.
的值.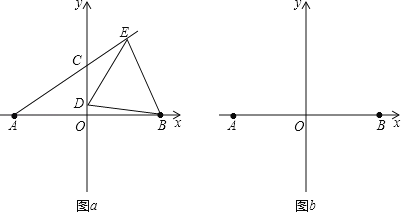
相关试题

