【题目】甲、乙在一段长2000米的直线公路上进行跑步练习,起跑时甲在起点,乙在甲的前面,若甲、乙同时起跑至甲到达终点的过程中,甲乙之间的距离y(米)与 时间x(秒)之间的函数关系如图所示.有下列说法:
①甲的速度为5米/秒;②100秒时甲追上乙;③经过50秒时甲乙相距50米;④甲到终点时,乙距离终点300米.其中正确的说法有( )

A. 4个 B. 3个
C. 2个 D. 1个
参考答案:
【答案】A
【解析】根据图象可以得到:开始跑时,两人相距100m,则起跑时乙在甲前面100m,在100秒时甲,乙的距离是0,则起跑后100秒甲追上乙, 甲每50秒比乙多跑100m,所以经过50秒时甲乙相距50米.
在100秒时甲,乙的距离是0,则起跑后100秒甲追上乙,故②说法正确;甲每100秒比乙多跑100m,所以经过50秒时甲乙相距50米,故③说法正确;甲每100秒比乙多跑100m,则在400秒时,相距300米,④说法正确;甲的速度为2000÷400=5m/s,故可以得出甲的速度为5m/s,故①正确.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”.

(1)已知:如图1,四边形ABCD的顶点A,B,C在网格格点上,请你在如下的5
 7的网格中画出3个不同形状的等邻边四边形ABCD,要求顶点D在网格格点上;
7的网格中画出3个不同形状的等邻边四边形ABCD,要求顶点D在网格格点上;(2)如图2,矩形ABCD中,AB=
 ,BC=5,点E在BC边上,连结DE画AF
,BC=5,点E在BC边上,连结DE画AF DE于点F,若DE=
DE于点F,若DE= CD,找出图中的等邻边四边形;
CD,找出图中的等邻边四边形;(3)如图3,在Rt
 ABC中,
ABC中, ACB=90°,AB=4,AC=2,D是BC的中点,点M是AB边上一点,当四边形ACDM是“等邻边四边形”时,求BM的长.
ACB=90°,AB=4,AC=2,D是BC的中点,点M是AB边上一点,当四边形ACDM是“等邻边四边形”时,求BM的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD的对角线长为2
 ,将正方形ABCD沿直线EF折叠,则图中阴影部分的周长为( )
,将正方形ABCD沿直线EF折叠,则图中阴影部分的周长为( )
A. 8
 B. 4
B. 4 C. 8 D. 6
C. 8 D. 6 -
科目: 来源: 题型:
查看答案和解析>>【题目】完全平方公式:(a±b)2=a2±2ab+b2适当的变形,可以解决很多的数学问题.
例如:若a+b=3,ab=1,求a2+b2的值.
解:因为a+b=3,ab=1
所以(a+b)2=9,2ab=2
所以a2+b2+2ab=9,2ab=2
得a2+b2=7
根据上面的解题思路与方法,解决下列问题:
(1)若(7﹣x)(x﹣4)=1,求(7﹣x)2+(x﹣4)2的值;
(2)如图,点C是线段AB上的一点,以AC、BC为边向两边作正方形,设AB=5,两正方形的面积和S1+S2=17,求图中阴影部分面积.

-
科目: 来源: 题型:
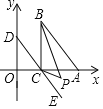
查看答案和解析>>【题目】如图,在直角坐标系中,三角形
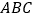 两顶点的坐标为
两顶点的坐标为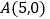 ,
,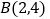 ,点
,点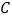 是
是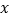 轴上一动点(不与点
轴上一动点(不与点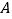 重合),过点
重合),过点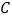 作
作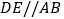 ,
,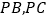 分别平分
分别平分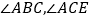 .
.
(1)当点
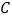 在点
在点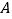 左边,三角形
左边,三角形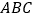 的面积为6时,求点
的面积为6时,求点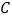 的坐标.
的坐标.(2)当
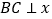 轴时,求
轴时,求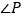 的度数.
的度数.(3)当点
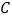 在点
在点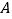 右边时,写出
右边时,写出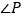 与
与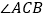 的数量关系(不用说理).
的数量关系(不用说理). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABO的顶点A是双曲线
 与直线
与直线 在第二象限的交点,AB⊥
在第二象限的交点,AB⊥ 轴于点B且S△ABO=
轴于点B且S△ABO= .
.(1)求这两个函数的解析式;
(2)求直线与双曲线的两个交点A,C的坐标;
(3)求△AOC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的直线交OP的延长线于点C,且CP=CB.
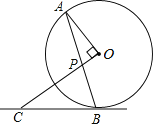
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为3,OP=1,求BC的长.
相关试题

