【题目】如图,Rt△ABO的顶点A是双曲线![]() 与直线
与直线![]() 在第二象限的交点,AB⊥
在第二象限的交点,AB⊥![]() 轴于点B且S△ABO=
轴于点B且S△ABO=![]() .
.
(1)求这两个函数的解析式;
(2)求直线与双曲线的两个交点A,C的坐标;
(3)求△AOC的面积.

参考答案:
【答案】(1)两个函数的解析式分别为y=![]() ,y=﹣x +2;(2)点A为(﹣1,3),C为(3,﹣1);(3)4
,y=﹣x +2;(2)点A为(﹣1,3),C为(3,﹣1);(3)4
【解析】试题分析:(1)根据S△ABO=![]() ,即
,即![]() ,所以
,所以![]() ,又因为图象在二四象限,所以xy=﹣3即k=-3,从而求出反比例函数解析式将k=-3代入
,又因为图象在二四象限,所以xy=﹣3即k=-3,从而求出反比例函数解析式将k=-3代入![]() ,求出一次函数解析式;
,求出一次函数解析式;
(2)将两个函数关系式y=﹣![]() 和y=﹣x +2联立,解这个方程组,可求出两个交点A,C的坐标;
和y=﹣x +2联立,解这个方程组,可求出两个交点A,C的坐标;
(3)将x=0代入y=﹣x +2中,求出D点坐标,根据△AOC的面积=△ADO的面积+△CDO的面积求解即可.
解:(1)设A点坐标为(x,y),且x<0,y>0
则S△ABO=![]() |OB||AB|=
|OB||AB|=![]() (﹣x)y=
(﹣x)y=![]()
∴xy=﹣3
又∵y=![]() ∴k=﹣3
∴k=﹣3
∴所求的两个函数的解析式分别为y=﹣![]() ,y=﹣x +2
,y=﹣x +2

(2)A、C两点坐标满足

解得 ![]()
∴交点A为(﹣1,3),C为(3,﹣1)
(3)由y=﹣x+2,令x=0,得y=2.
∴直线y=﹣x+2与y轴的交点D的坐标为(0,2)
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】完全平方公式:(a±b)2=a2±2ab+b2适当的变形,可以解决很多的数学问题.
例如:若a+b=3,ab=1,求a2+b2的值.
解:因为a+b=3,ab=1
所以(a+b)2=9,2ab=2
所以a2+b2+2ab=9,2ab=2
得a2+b2=7
根据上面的解题思路与方法,解决下列问题:
(1)若(7﹣x)(x﹣4)=1,求(7﹣x)2+(x﹣4)2的值;
(2)如图,点C是线段AB上的一点,以AC、BC为边向两边作正方形,设AB=5,两正方形的面积和S1+S2=17,求图中阴影部分面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙在一段长2000米的直线公路上进行跑步练习,起跑时甲在起点,乙在甲的前面,若甲、乙同时起跑至甲到达终点的过程中,甲乙之间的距离y(米)与 时间x(秒)之间的函数关系如图所示.有下列说法:
①甲的速度为5米/秒;②100秒时甲追上乙;③经过50秒时甲乙相距50米;④甲到终点时,乙距离终点300米.其中正确的说法有( )

A. 4个 B. 3个
C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,三角形
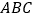 两顶点的坐标为
两顶点的坐标为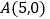 ,
,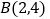 ,点
,点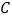 是
是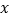 轴上一动点(不与点
轴上一动点(不与点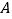 重合),过点
重合),过点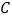 作
作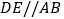 ,
,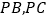 分别平分
分别平分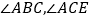 .
.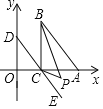
(1)当点
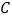 在点
在点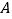 左边,三角形
左边,三角形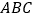 的面积为6时,求点
的面积为6时,求点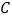 的坐标.
的坐标.(2)当
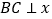 轴时,求
轴时,求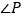 的度数.
的度数.(3)当点
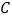 在点
在点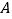 右边时,写出
右边时,写出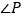 与
与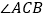 的数量关系(不用说理).
的数量关系(不用说理). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的直线交OP的延长线于点C,且CP=CB.
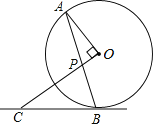
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为3,OP=1,求BC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,对角线AC,BD相交于点O,AC=12,BD=16,E为AD中点,点P在x轴上移动.若△POE为等腰三角形,请写出所有符合要求的点P的坐标 .

-
科目: 来源: 题型:
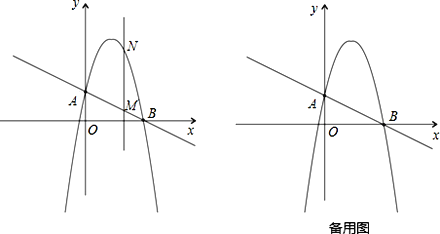
查看答案和解析>>【题目】如图,一次函数
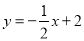 分别交y轴、x 轴于A、B两点,抛物线
分别交y轴、x 轴于A、B两点,抛物线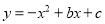 过A、B两点.
过A、B两点.(1)求这个抛物线的解析式;
(2)作垂直x轴的直线x=t,在第一象限交直线AB于点M,交这个抛物线于点N.求当t 取何值时,MN有最大值?最大值是多少?
(3)在(2)的情况下,以A、M、N、D为顶点作平行四边形,求第四个顶点D的坐标.
相关试题

