Question

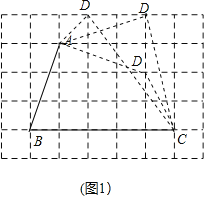
【题目】我们定义：有一组邻边相等的凸四边形叫做“等邻边四边形”．

（1）已知：如图1，四边形ABCD的顶点A，B，C在网格格点上，请你在如下的57的网格中画出3个不同形状的等邻边四边形ABCD，要求顶点D在网格格点上；

（2）如图2，矩形ABCD中，AB=，BC=5，点E在BC边上，连结DE画AFDE于点F，若DE=CD，找出图中的等邻边四边形；

（3）如图3，在RtABC中，ACB=90°，AB=4，AC=2，D是BC的中点，点M是AB边上一点，当四边形ACDM是“等邻边四边形”时，求BM的长．

Answer 1

【答案】（1）见解析；（2）四边形ABEF和四边形ABED都是等邻边四边形；（3）当BM为2或3或时，四边形ACDM是“等邻边四边形”．

【解析】

（1）根据”等邻边四边形”的定义画出3个不同形状的等邻边四边形；

（2）根据题意求出DE，根据勾股定理求出CE，计算得到BE=AB，根据等邻边四边形的定义判断即可；

（3）分AM=AC、DM=DC、MA=MD三种情况，根据勾股定理、等腰三角形的性质计算即可．

（1）3个不同形状的等邻边四边形ABCD如图所示：

（2）四边形ABEF和四边形ABED都是等邻边四边形，

∵四边形ABCD是矩形，

∴AD=BC=5，CD=AB=，

∴DE=CD=，

由勾股定理得，CE==，

∴BE=BC-CE=5-=，

∴BE=AB，

∴四边形ABEF和四边形ABED都是等邻边四边形；

（3）①当AM=AC时，BM=2；

②当DM=DC时，如图3，作DH⊥AB于H，

∵∠ACB=90°，AB=4，AC=2，

∴BC=，∠B=30°，

∴BD=DM=，

在Rt△BDH中，BH=BD×cosB=，

∵DM=DB，DH⊥AB，

∴BM=2BH=3；

③当MA=MD时，如图4，作DH⊥AB于H，

设MA=MD=x，

由②得，BH=，DH=，

则MH=4-x-=-x，

在Rt△MDH中，DM2=MH2+DH2，即x2=（-x）2+（）2，

解得，x=，即AM=，

∴BM=4-=，

综上所述，当BM为2或3或时，四边形ACDM是“等邻边四边形”．