【题目】完全平方公式:(a±b)2=a2±2ab+b2适当的变形,可以解决很多的数学问题.
例如:若a+b=3,ab=1,求a2+b2的值.
解:因为a+b=3,ab=1
所以(a+b)2=9,2ab=2
所以a2+b2+2ab=9,2ab=2
得a2+b2=7
根据上面的解题思路与方法,解决下列问题:
(1)若(7﹣x)(x﹣4)=1,求(7﹣x)2+(x﹣4)2的值;
(2)如图,点C是线段AB上的一点,以AC、BC为边向两边作正方形,设AB=5,两正方形的面积和S1+S2=17,求图中阴影部分面积.

参考答案:
【答案】(1)7;(2)S阴影=2.
【解析】
(1)把7-x与x-4分别看作ab,则a+b=3,ab=1,再按题中的思路求解即可;
(2)先根据a2+b2=(a+b)2﹣2ab求出ab的值,然后根据三角形面积公式可得结论.
解:(1)∵(7﹣x)(x﹣4)=1,(7﹣x)+(x﹣4)=7﹣x+x﹣4=3
由例题的解法可得:
(7﹣x)2+(x﹣4)2=[(7﹣x)+(x﹣4)]2-2(7﹣x)(x﹣4)=32-2=7;
(2)设AC=a,BC=CF=b,
则a+b=5,a2+b2=17,
∴a2+b2=(a+b)2﹣2ab,
17=25﹣2ab,
ab=4,
∴S阴影=![]() ab=2.
ab=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:
中华优秀传统文化是中华民族的“根”和“魂”.为传承优秀传统文化,某校购进《西游记》和《三国演义》若干套,其中每套《西游记》的价格比每套《三国演义》的价格多40元,用3200元购买《三国演义》的套数是用2400元购买《西游记》套数的2倍,求每套《三国演义》的价格.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校提倡练字,小冬和小红一起去文具店买钢笔和字帖,小冬在文具店买1支钢笔和3本字帖共花了38元,小红买了2支钢笔和4本字帖共花了64元.
(1)每支钢笔与每本字帖分别多少元?
(2)帅帅在六一节当天去买,正巧碰到文具店搞促销,促销方案有两种形式:
①所购商品均打九折
②买一支钢笔赠送一本字帖
帅帅要买5支钢笔和15本字帖,他有三种选择方案:
(Ⅰ)一次买5支钢笔和15本字帖,然后按九折付费;
(Ⅱ)一次买5支钢笔和10本字帖,文具店再赠送5本字帖;
(Ⅲ)分两次购买,第一次买5支钢笔,文具店会赠送5本字帖,第二次再去买10本字帖,可以按九折付费;问帅帅最少要付多少钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+2x+3与x轴交于A、B两点,与y轴交于C点,对称轴与抛物线相交于点M,与x轴相交于点N.点P是线段MN上的一动点,过点P作PE⊥CP交x轴于点E.
(1)直接写出抛物线的顶点M的坐标是 .
(2)当点E与点O(原点)重合时,求点P的坐标.
(3)点P从M运动到N的过程中,求动点E的运动的路径长.

-
科目: 来源: 题型:
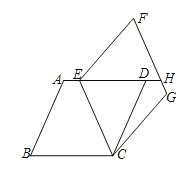
查看答案和解析>>【题目】如图,完全相同的两个菱形ABCD和ECGF的顶点C重合,∠B=∠F,点E恰好在边AD上,延长ED交FG于点H.
(1)求证:∠B=∠ECB;
(2)连接BE、CH.
①试判断四边形BEHC的形状,并说理理由;
②求证:CH平分∠DCG.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax2+bx+c的顶点为D(﹣1,2),与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则以下结论:①b2﹣4ac<0;②当x>﹣1时,y随x增大而减小;③a+b+c<0;④若方程ax2+bx+c﹣m=0没有实数根,则m>2; ⑤3a+c<0.其中正确结论的个数是( )

A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】(4分)如图,直线l外不重合的两点A、B,在直线l上求作一点C,使得AC+BC的长度最短,作法为:①作点B关于直线l的对称点B′;②连接AB′与直线l相交于点C,则点C为所求作的点.在解决这个问题时没有运用到的知识或方法是( )

A.转化思想
B.三角形的两边之和大于第三边
C.两点之间,线段最短
D.三角形的一个外角大于与它不相邻的任意一个内角
相关试题

