【题目】(1)如图1,在Rt△ABC中,∠ACB=90°,∠A=60°,CD平分∠ACB.
求证:CA+AD=BC.
小明为解决上面的问题作了如下思考:作△ADC关于直线CD的对称图形△A′DC,
∵CD平分∠ACB,∴A′点落在CB上,且CA′=CA,A′D=AD.因此,要证的问题转化为只要证A′D=A′B.请根据小明的思考写出该问题完整的证明过程.
(2)参照(1)中小明的思考方法,解答下列问题:
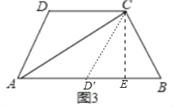
如图3,在四边形ABCD中,AC平分∠BAD,BC=CD=10,AC=17,AD=9,求AB的长.

参考答案:
【答案】(1)见解析;(2)21.
【解析】
(1)作△ADC关于CD的对称图形△A′DC,再证明AD=BA′即可;
(2)如图,作△ADC关于AC的对称图形△A′DC.过点C作CE⊥AB于点E,则D′E=BE.设D′E=BE=x.在Rt△CEB中,CE2=CB2﹣BE2=102﹣x2,在Rt△CEA中,CE2=AC2﹣AE2=172﹣(9+x)2.由此构建方程即可解决问题;
(1)证明:作△ADC关于CD的对称图形△A′DC,
∴△ADC≌△A′DC,
∴A′D=AD,C A′=CA,∠CA′D=∠A=60°,
∵CD平分∠ACB,
∴A′点落在CB上
∵∠ACB=90°,
∴∠B=90°﹣∠A=30°,
∵CD平分∠ACB,
∴∠ACD=45°
在△ACD中,∠ADC=180°﹣∠A﹣∠A CD=75°
∴∠A′DC=∠ADC=75°,
∴∠A′DB=180°﹣∠ADC﹣∠A′DC=30°,
∴∠A′DB=∠B,∴A′D=A′B,
∴CA+AD=CA′+A′D=C A′+A′B=CB.
(2)如图,作△ADC关于AC的对称图形△A′DC.
∴△ADC≌△A′DC,
∴D′A=DA=9,D′C=DC=10,
∵AC平分∠BAD,∴D′点落在AB上,
∵BC=10,∴D′C=BC,
过点C作CE⊥AB于点E,则D′E=BE.
设D′E=BE=x.
在Rt△CEB中,CE2=CB2﹣BE2=102﹣x2,
在Rt△CEA中,CE2=AC2﹣AE2=172﹣(9+x)2.
∴102﹣x2=172﹣(9+x)2,
解得:x=6,
∴AB=AD′+D′E+EB=9+6+6=21.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)某工厂计划在规定时间内生产24000个零件,若每天比原计划多生产30个零件,则在规定时间内可以多生产300个零件.
(1)求原计划每天生产的零件个数和规定的天数.
(2)为了提前完成生产任务,工厂在安排原有工人按原计划正常生产的同时,引进5组机器人生产流水线共同参与零件生产,已知每组机器人生产流水线每天生产零件的个数比20个工人原计划每天生产的零件总数还多20%,按此测算,恰好提前两天完成24000个零件的生产任务,求原计划安排的工人人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年初,东北遭遇了几次大量降雪天气,某市出动了多辆清雪车连夜清雪.大型清雪车比小型清雪车每小时多清扫路面6 km,大型清雪车清扫路面90 km与小型清雪车清扫路面60 km所用的时间相同,求小型清雪车每小时清扫路面的长度.
-
科目: 来源: 题型:
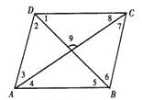
查看答案和解析>>【题目】如图,∠3和∠9是直线________、_______被直线_______所截而成的______角;∠6和∠9是直线_____、______被直线________所截而成的_______角.
-
科目: 来源: 题型:
查看答案和解析>>【题目】)已知,AB和DE是直立在地面上的两根立柱,AB=6m,某一时刻AB在阳光下的投影BC=4m.
(1)请你在图中画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为8m,请你计算DE的长.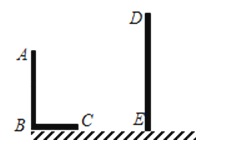
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l上有三个正方形a,b,c,若a,c的面积分别为2和10,则b的面积为( )

A. 8 B.
 C.
C.  D. 12
D. 12 -
科目: 来源: 题型:
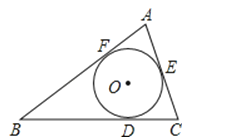
查看答案和解析>>【题目】在三角形ABC中,BC=14,AC=9,AB=13,它的内切圆分别和BC、AC、AB切于点D、E、F,那么AF、BD、CE的长分别为( )
A.AF=4,BD=9,CE=5
B.AF=4,BD=5,CE=9
C.AF=5,BD=4,CE=9
D.AF=9,BD=4,CE=5
相关试题

