【题目】)已知,AB和DE是直立在地面上的两根立柱,AB=6m,某一时刻AB在阳光下的投影BC=4m.
(1)请你在图中画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为8m,请你计算DE的长.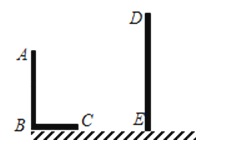
参考答案:
【答案】解:(1)连接AC,过点D作DF∥AC,交直线BC于点F,线段EF即为DE的投影.
(2)∵AC∥DF,
∴∠ACB=∠DFE.
∵∠ABC=∠DEF=90°
∴△ABC∽△DEF.
∴AB:DE=BC:EF,
∵AB=6m,BC=4m,EF=8
∴6:4=DE:8
∴DE=12(m).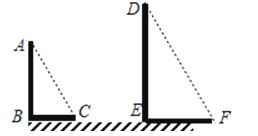
【解析】(1)根据投影的定义,作出投影即可;
(2)根据在同一时刻,不同物体的物高和影长成比例;构造比例关系AB:DE=BC:EF.计算可得DE=10(m).
【考点精析】认真审题,首先需要了解相似三角形的应用(测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解),还要掌握平行投影(太阳光线可以看成是平行光线,平行光线所形成的投影称为平行投影;作物体的平行投影:由于平行投影的光线是平行的,而物体的顶端与影子的顶端确定的直线就是光线,故根据另一物体的顶端可作出其影子)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年初,东北遭遇了几次大量降雪天气,某市出动了多辆清雪车连夜清雪.大型清雪车比小型清雪车每小时多清扫路面6 km,大型清雪车清扫路面90 km与小型清雪车清扫路面60 km所用的时间相同,求小型清雪车每小时清扫路面的长度.
-
科目: 来源: 题型:
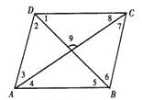
查看答案和解析>>【题目】如图,∠3和∠9是直线________、_______被直线_______所截而成的______角;∠6和∠9是直线_____、______被直线________所截而成的_______角.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,在Rt△ABC中,∠ACB=90°,∠A=60°,CD平分∠ACB.
求证:CA+AD=BC.
小明为解决上面的问题作了如下思考:作△ADC关于直线CD的对称图形△A′DC,
∵CD平分∠ACB,∴A′点落在CB上,且CA′=CA,A′D=AD.因此,要证的问题转化为只要证A′D=A′B.请根据小明的思考写出该问题完整的证明过程.
(2)参照(1)中小明的思考方法,解答下列问题:
如图3,在四边形ABCD中,AC平分∠BAD,BC=CD=10,AC=17,AD=9,求AB的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l上有三个正方形a,b,c,若a,c的面积分别为2和10,则b的面积为( )

A. 8 B.
 C.
C.  D. 12
D. 12 -
科目: 来源: 题型:
查看答案和解析>>【题目】在三角形ABC中,BC=14,AC=9,AB=13,它的内切圆分别和BC、AC、AB切于点D、E、F,那么AF、BD、CE的长分别为( )
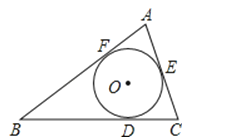
A.AF=4,BD=9,CE=5
B.AF=4,BD=5,CE=9
C.AF=5,BD=4,CE=9
D.AF=9,BD=4,CE=5 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若AD∥BC,AB∥DE,DF∥AC,∠OEC=72°,∠OCE=64°,则∠B=_______,∠F=_______,∠BAD=_______,∠ADF=_______.

相关试题

