【题目】为迎接中国森博会,某商家计划从厂家采购A,B两种产品共20件,产品的采购单价(元/件)是采购数量(件)的一次函数,下表提供了部分采购数据.
采购数量(件) | 1 | 2 | … |
A产品单价(元/件) | 1480 | 1460 | … |
B产品单价(元/件) | 1290 | 1280 | … |
(1)设A产品的采购数量为x(件),采购单价为y1(元/件),求y1与x的关系式;
(2)经商家与厂家协商,采购A产品的数量不少于B产品数量的![]() ,且A产品采购单价不低于1200元,求该商家共有几种进货方案;
,且A产品采购单价不低于1200元,求该商家共有几种进货方案;
(3)该商家分别以1760元/件和1700元/件的销售单价售出A,B两种产品,且全部售完,在(2)的条件下,求采购A种产品多少件时总利润最大,并求最大利润.
参考答案:
【答案】(1)y1=﹣20x+1500(0<x≤20,x为整数);(2)商家共有5种进货方案;(3)当x=15时,W最大=10650.
【解析】试题分析:(1)首先设出函数解析式,然后根据表格将数字代入进行求解;(2)根据题意列出关于x的不等式组,然后根据x为整数,求出x的值;(3)设总利润为w,列出w和x的二次函数关系式,然后根据二次函数的增减性进行求解.
试题解析:(1)设y1与x的关系式y1=kx+b,由表知![]() ,
,
解得k=﹣20,b=1500, 即y1=﹣20x+1500(0<x≤20,x为整数),
(2)根据题意可得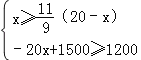 , 解得11≤x≤15, ∵x为整数,
, 解得11≤x≤15, ∵x为整数,
∴x可取的值为:11,12,13,14,15, ∴该商家共有5种进货方案;
(3)令总利润为W,则W=30x2﹣540x+1200=30(x﹣9)2+9570,
∵a=30>0, ∴当x≥9时,W随x的增大而增大, ∵11≤x≤15,
∴当x=15时,W最大=10650;
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=(x-m)2-(x-m),其中m是常数.
(1)求证:不论m为何值,该抛物线与x轴一定有两个公共点;
(2)若该抛物线的对称轴为直线x=
 .
.①求该抛物线的函数解析式;
②把该抛物线沿y轴向上平移多少个单位长度后,得到的抛物线与x轴只有一个公共点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学准备搬入新校舍,在迁入新校舍前就该校300名学生如何到校问题进行了一次调查,并得到如下数据:
步行
65人
骑自行车
100人
坐公共汽车
125人
其他
10人
将上面的数据分别制成扇形统计图和条形统计图.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,小聪在学习圆的性质时发现一个结论,△ABC内接于⊙O,AD⊥BC,则∠BAD=∠OAC.
(1)请你帮小聪证明这个结论;
(2)运用以上结论解决问题:如图②,H为△ABC的垂心,若∠ABC的平分线BE⊥HO,⊙O的半径为10,求弦AC的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,点E为AB中点,连接CE,将顶点B沿CE折叠至点P处,连接AP并延长交边CD于点F,
(1)判断四边形AECF为的形状并说明理由;
(2)若点P同时可看作是B点绕C点顺时针旋转60°得到,求证:△APB≌△ECP;
(3)若AB=6,BC=4,求
 的值
的值 
-
科目: 来源: 题型:
查看答案和解析>>【题目】(14分)如图,已知抛物线
 (
( )与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C,且OC=OB.
)与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C,且OC=OB.
(1)求此抛物线的解析式;
(2)若点E为第二象限抛物线上一动点,连接BE,CE,求四边形BOCE面积的最大值,并求出此时点E的坐标;
(3)点P在抛物线的对称轴上,若线段PA绕点P逆时针旋转90°后,点A的对应点A′恰好也落在此抛物线上,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在购买某场足球门票时,设购买门票数为x(张),费用为y(元).现有两种购买方案:
方案一:若单位费助广告费10000元,则该单位所购门票的价格为每张60元;(总费用=广告赞助费+门票费)
方案二:购买门票方式如图所示.
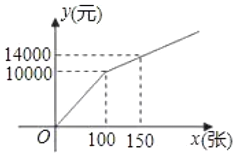
解答下列问题:
(1)方案一中,y与x的函数关系式为 ;
方案二中,当0
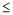 x
x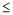 100时,y与x的函数关系式为 ;
100时,y与x的函数关系式为 ;当x>100时,y与x的函数关系式为 ;
(2)如果购买本场足球赛门票超过100张,你将选择哪一种方案,使总费用最省?请说明理由.
相关试题

