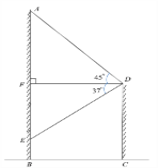
【题目】如图,在建筑物AB上,挂着35 m长的宣传条幅AE,从另一建筑物CD的顶部D处看条幅顶端A处,仰角为45°,看条幅底端E处,俯角为37°.求两建筑物间的距离BC.
(参考数据:sin37°≈0.6,cos37°≈0.8, tan37°≈0.75)

参考答案:
【答案】两建筑物间的距离BC为20m
【解析】试题分析:
如图,过点D作DF![]() AB交AB于点F,则∠DFA=∠DFE=90°,结合已知条件易得AF=DF,EF=DF·tan37°,结合AE=AF+EF=35即可列出方程解得DF的长,这样由四边形BCDF是矩形即可得到BC=DF从而求出BC的长了.
AB交AB于点F,则∠DFA=∠DFE=90°,结合已知条件易得AF=DF,EF=DF·tan37°,结合AE=AF+EF=35即可列出方程解得DF的长,这样由四边形BCDF是矩形即可得到BC=DF从而求出BC的长了.
试题解析:
过点D作DF![]() AB交AB于点F,
AB交AB于点F,
∴∠DFA=∠DFE=90°,
∵∠ABC=∠BCD=90°,
∴四边形BCDF是矩形,
∴BC=DF,
∵在Rt△ADF中,∠ADF=45°,
∴AF=DF,
∵在Rt△DFE中,∠EDF=37°,
∴EF=DF·tan37°,
又∵AF+EF=AE=35,
∴DF+DF·tan37°=35,
解得DF=BC=20(m)
答:两建筑物间的距离BC为20m.
-
科目: 来源: 题型:
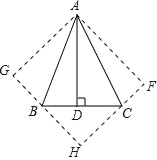
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=45°,AD⊥BC于D,将△ACD沿AC折叠为△ACF,将△ABD沿AB折叠为△ABG,延长FC和GB相交于点H.
(1)求证:四边形AFHG为正方形;
(2)若BD=6,CD=4,求AB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了培养学生的兴趣,我市某小学决定再开设A.舞蹈,B.音乐,C.绘画,D.书法四个兴趣班,为了解学生对这四个项目的兴趣爱好,随机抽取了部分学生进行调查,并将调查结果绘制成如图1,2所示的统计图,且结合图中信息解答下列问题:

(1)在这次调查中,共调查了多少名学生?
(2)请将两幅统计图补充完整;
(3)若本校一共有2000名学生,请估计喜欢“音乐”的人数;
(4)若调查到喜欢“书法”的4名学生中有2名男生,2名女生,现从这4名学生中任意抽取2名学生,请用画树状图或列表的方法,求出刚好抽到相同性别的学生的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,△ABC与△CDE是等腰直角三角形,直角边AC、CD在同一条直线上,点M,N分别是斜边AB,DE的中点,点P为AD的中点,连接AE、BD、MN.
(1)求证:△PMN为等腰直角三角形;
(2)现将图①中的△CDE绕着点C顺时针旋转α(0°<α<90°),得到图②,AE与MP,BD分别交于点G、H,请判断①中的结论是否成立,若成立,请证明;若不成立,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知点
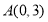 ,
,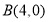 ,
,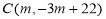 ,点
,点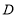 与
与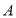 关于
关于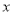 轴对称.
轴对称.(1)写出点
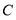 所在直线的函数解析式;
所在直线的函数解析式;(2)连接
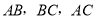 ,若线段
,若线段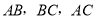 能构成三角形,求
能构成三角形,求 的取值范围;
的取值范围;(3)若直线
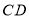 把四边形
把四边形 的面积分成相等的两部分,试求
的面积分成相等的两部分,试求 的值.
的值.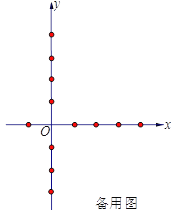
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是小明化简分式的过程,仔细阅读并解答所提出的问题
解:
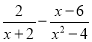
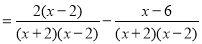 第一步
第一步=2(x2)(x6)第二步
=2x4x6第三步
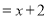 第四步
第四步(1)小明的解法从第 步开始出现错误;
(2)第一步进行 ,它的数学依据是 .
(3)第三步进行 ,它的数学依据是 .
(4)正确的化简结果是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的顶点A在第一象限,AB∥x轴,AD∥y轴,且对角线的交点与原点重合,在边AB从小于AD到大于AD的变化过程中,若矩形ABCD的周长始终保持不变,则经过动点A的反比例函数
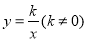 中,k的值的变化情况是( )
中,k的值的变化情况是( )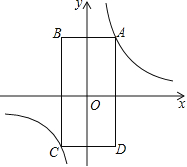
A. 一直增大B. 一直减小C. 先增大后减小D. 先减小后增大
相关试题

