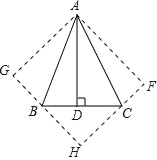
【题目】如图,在△ABC中,∠BAC=45°,AD⊥BC于D,将△ACD沿AC折叠为△ACF,将△ABD沿AB折叠为△ABG,延长FC和GB相交于点H.
(1)求证:四边形AFHG为正方形;
(2)若BD=6,CD=4,求AB的长.
参考答案:
【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)由折叠的性质可得到的条件是:①AG=AD=AF,②∠GAF=∠GAD+∠DAF=2∠BAC=90°,且∠G=∠F=90°;由②可判定四边形AGHF是矩形,由AG=AF可证得四边形AGHF是正方形;
(2)设AD=x,由折叠的性质可得:AD=AF=x(即正方形的边长为x),BG=BD=6,CF=CD=4;进而可用x表示出BH、HC的长,即可在Rt△BHC中,由勾股定理求得AD的长,进而可求出AB的长.
试题解析:(1)∵AD⊥BC,
∴∠ADB=∠ADC=90°;
由折叠可知,AG=AF=AD,∠AGH=∠AFH=90°,
∠BAG=∠BAD,∠CAF=∠CAD,
∴∠BAG+∠CAF=∠BAD+∠CAD=∠BAC=45°;
∴∠GAF=∠BAG+∠CAF+∠BAC=90°;
∴四边形AFHG是正方形;
(2)∵四边形AFHG是正方形,
∴∠BHC=90°,
又GH=HF=AD,GB=BD=6,CF=CD=4,
设AD的长为x,则BH=GH﹣GB=x﹣6,CH=HF﹣CF=x﹣4,
在Rt△BCH中,BH2+CH2=BC2,
∴(x﹣6)2+(x﹣4)2=102,
解得x1=12,x2=﹣2(不合题意,舍去),
∴AD=12,
∴AB=![]() .
.
-
科目: 来源: 题型:
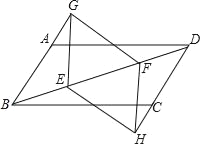
查看答案和解析>>【题目】如图,在ABCD中,E、F是对角线BD上的两点,BE=DF,点G、H分别在BA和DC的延长线上,且AG=CH,连接GE、EH、HF、FG.
求证:(1)△BEG≌△DFH;
(2)四边形GEHF是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】.观察下列算式特点:
①13=12
②13+23=32
③13+23+33=62
④13+23+33+43=102
⑤13+23+33+43+53=152…
(1)请你写出第⑥个算式;
(2)用含n(n为正整数)的式子表示第n个算式;
(3)请用上述规律计算:73+83+93+…+123.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知矩形ABCD的长AB=2,AB边与x轴重合,双曲线y=
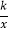 在第一象限内经过D点以及BC的中点E.
在第一象限内经过D点以及BC的中点E.(1)求A点的横坐标;
(2)连接ED,若四边形ABED的面积为6,求双曲线的函数关系式.
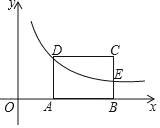
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了培养学生的兴趣,我市某小学决定再开设A.舞蹈,B.音乐,C.绘画,D.书法四个兴趣班,为了解学生对这四个项目的兴趣爱好,随机抽取了部分学生进行调查,并将调查结果绘制成如图1,2所示的统计图,且结合图中信息解答下列问题:

(1)在这次调查中,共调查了多少名学生?
(2)请将两幅统计图补充完整;
(3)若本校一共有2000名学生,请估计喜欢“音乐”的人数;
(4)若调查到喜欢“书法”的4名学生中有2名男生,2名女生,现从这4名学生中任意抽取2名学生,请用画树状图或列表的方法,求出刚好抽到相同性别的学生的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,△ABC与△CDE是等腰直角三角形,直角边AC、CD在同一条直线上,点M,N分别是斜边AB,DE的中点,点P为AD的中点,连接AE、BD、MN.
(1)求证:△PMN为等腰直角三角形;
(2)现将图①中的△CDE绕着点C顺时针旋转α(0°<α<90°),得到图②,AE与MP,BD分别交于点G、H,请判断①中的结论是否成立,若成立,请证明;若不成立,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在建筑物AB上,挂着35 m长的宣传条幅AE,从另一建筑物CD的顶部D处看条幅顶端A处,仰角为45°,看条幅底端E处,俯角为37°.求两建筑物间的距离BC.
(参考数据:sin37°≈0.6,cos37°≈0.8, tan37°≈0.75)

相关试题

