【题目】在平面直角坐标系中,已知点![]() ,
,![]() ,
,![]() ,点
,点![]() 与
与![]() 关于
关于![]() 轴对称.
轴对称.
(1)写出点![]() 所在直线的函数解析式;
所在直线的函数解析式;
(2)连接![]() ,若线段
,若线段![]() 能构成三角形,求
能构成三角形,求![]() 的取值范围;
的取值范围;
(3)若直线![]() 把四边形
把四边形![]() 的面积分成相等的两部分,试求
的面积分成相等的两部分,试求![]() 的值.
的值.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() 时,线段
时,线段![]() 能构成三角形;(3)当
能构成三角形;(3)当![]() 时,
时,![]() 把四边形
把四边形![]() 的面积分成相等的两部分.
的面积分成相等的两部分.
【解析】
(1)根据题意可得点![]() ,可得的当横坐标为m时,纵坐标为-3m+22,因此可得点C的所在直线的解析式.
,可得的当横坐标为m时,纵坐标为-3m+22,因此可得点C的所在直线的解析式.
(2)首先利用待定系数法计算直线AB的解析式,再利用点C是否在直线上,来确定是否构成三角形,从而确定m的范围.
(3)首先计算D点坐标,设![]() 的中点为
的中点为![]() ,过
,过![]() 作
作![]()
![]() 轴于
轴于![]() ,
,![]()
![]() 轴于
轴于![]() ,进而确定E点的坐标,再计算DE所在直线的解析式,根据点C在直线DE上可求得m的值.
,进而确定E点的坐标,再计算DE所在直线的解析式,根据点C在直线DE上可求得m的值.
解:(1)根据题意可得点![]() ,可得的当横坐标为m时,纵坐标为-3m+22,所以
,可得的当横坐标为m时,纵坐标为-3m+22,所以![]()
(2)设![]() 所在直线的函数解析式为
所在直线的函数解析式为![]() ,将点
,将点![]() ,
,![]() 代入
代入![]() 得
得
![]() ,解得
,解得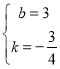 ,∴
,∴![]()
当点![]() 在直线
在直线![]() 上时,线段
上时,线段![]() 不能构成三角形
不能构成三角形
将![]() 代入
代入![]() ,得
,得![]()
解得![]() ,
,
∴![]() 时,线段
时,线段![]() 能构成三角形;
能构成三角形;
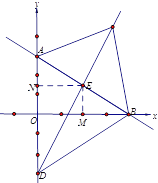
(3)根据题意可得![]() ,
,
设![]() 的中点为
的中点为![]() ,过
,过![]() 作
作![]()
![]() 轴于
轴于![]() ,
,![]()
![]() 轴于
轴于![]() ,
,
根据三角形中位线性质可知![]() ,由三角形中线性质可知,当点
,由三角形中线性质可知,当点![]() 在直线
在直线![]() 上时,
上时,![]() 把四边形
把四边形![]() 的面积分成相等的两部分,
的面积分成相等的两部分,
设直线![]() 的函数解析式为
的函数解析式为![]() ,将
,将![]() ,
,![]() 代入
代入![]() ,
,
得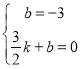 ,解得
,解得![]() ,∴
,∴![]() ,
,
将![]() 代入
代入![]() ,得
,得
![]() ,解得
,解得![]() ,
,
∴当![]() 时,
时,![]() 把四边形
把四边形![]() 的面积分成相等的两部分.
的面积分成相等的两部分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了培养学生的兴趣,我市某小学决定再开设A.舞蹈,B.音乐,C.绘画,D.书法四个兴趣班,为了解学生对这四个项目的兴趣爱好,随机抽取了部分学生进行调查,并将调查结果绘制成如图1,2所示的统计图,且结合图中信息解答下列问题:

(1)在这次调查中,共调查了多少名学生?
(2)请将两幅统计图补充完整;
(3)若本校一共有2000名学生,请估计喜欢“音乐”的人数;
(4)若调查到喜欢“书法”的4名学生中有2名男生,2名女生,现从这4名学生中任意抽取2名学生,请用画树状图或列表的方法,求出刚好抽到相同性别的学生的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,△ABC与△CDE是等腰直角三角形,直角边AC、CD在同一条直线上,点M,N分别是斜边AB,DE的中点,点P为AD的中点,连接AE、BD、MN.
(1)求证:△PMN为等腰直角三角形;
(2)现将图①中的△CDE绕着点C顺时针旋转α(0°<α<90°),得到图②,AE与MP,BD分别交于点G、H,请判断①中的结论是否成立,若成立,请证明;若不成立,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在建筑物AB上,挂着35 m长的宣传条幅AE,从另一建筑物CD的顶部D处看条幅顶端A处,仰角为45°,看条幅底端E处,俯角为37°.求两建筑物间的距离BC.
(参考数据:sin37°≈0.6,cos37°≈0.8, tan37°≈0.75)

-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是小明化简分式的过程,仔细阅读并解答所提出的问题
解:
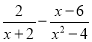
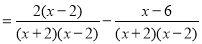 第一步
第一步=2(x2)(x6)第二步
=2x4x6第三步
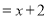 第四步
第四步(1)小明的解法从第 步开始出现错误;
(2)第一步进行 ,它的数学依据是 .
(3)第三步进行 ,它的数学依据是 .
(4)正确的化简结果是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的顶点A在第一象限,AB∥x轴,AD∥y轴,且对角线的交点与原点重合,在边AB从小于AD到大于AD的变化过程中,若矩形ABCD的周长始终保持不变,则经过动点A的反比例函数
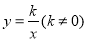 中,k的值的变化情况是( )
中,k的值的变化情况是( )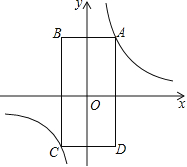
A. 一直增大B. 一直减小C. 先增大后减小D. 先减小后增大
-
科目: 来源: 题型:
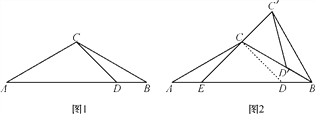
查看答案和解析>>【题目】如图1,△ABC中,AC=BC,∠A=30°,点D在AB边上,且∠ADC=45°.
(1)求∠BCD的度数;
(2)将图1中的△BCD绕点B顺时针旋转得到△BC′D′,当点D′恰好落在BC边上时,如图2所示,连接C′C并延长交AB于点E.
①求∠C′CB的度数;
②求证:△C′BD′≌△CAE.
相关试题

