【题目】如图,矩形ABCD的顶点A在第一象限,AB∥x轴,AD∥y轴,且对角线的交点与原点重合,在边AB从小于AD到大于AD的变化过程中,若矩形ABCD的周长始终保持不变,则经过动点A的反比例函数![]() 中,k的值的变化情况是( )
中,k的值的变化情况是( )
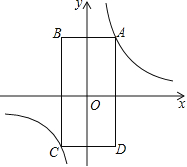
A. 一直增大B. 一直减小C. 先增大后减小D. 先减小后增大
参考答案:
【答案】C
【解析】
试题设矩形ABCD中,AB=2a,AD=2b.矩形ABCD的周长始终保持不变,矩形的周长2(2a+2b)=4(a+b)为定值,可得a+b为定值.又因矩形对角线的交点与原点O重合,可得k=![]() AB
AB![]() AD=ab,a+b为定值时,当a=b时,ab最大,所以在边AB从小于AD到大于AD的变化过程中,k的值先增大后减小.故答案选C.
AD=ab,a+b为定值时,当a=b时,ab最大,所以在边AB从小于AD到大于AD的变化过程中,k的值先增大后减小.故答案选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在建筑物AB上,挂着35 m长的宣传条幅AE,从另一建筑物CD的顶部D处看条幅顶端A处,仰角为45°,看条幅底端E处,俯角为37°.求两建筑物间的距离BC.
(参考数据:sin37°≈0.6,cos37°≈0.8, tan37°≈0.75)

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知点
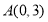 ,
,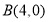 ,
,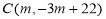 ,点
,点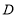 与
与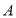 关于
关于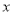 轴对称.
轴对称.(1)写出点
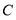 所在直线的函数解析式;
所在直线的函数解析式;(2)连接
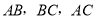 ,若线段
,若线段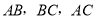 能构成三角形,求
能构成三角形,求 的取值范围;
的取值范围;(3)若直线
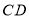 把四边形
把四边形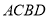 的面积分成相等的两部分,试求
的面积分成相等的两部分,试求 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是小明化简分式的过程,仔细阅读并解答所提出的问题
解:
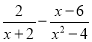
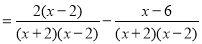 第一步
第一步=2(x2)(x6)第二步
=2x4x6第三步
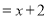 第四步
第四步(1)小明的解法从第 步开始出现错误;
(2)第一步进行 ,它的数学依据是 .
(3)第三步进行 ,它的数学依据是 .
(4)正确的化简结果是 .
-
科目: 来源: 题型:
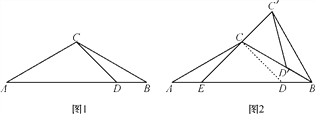
查看答案和解析>>【题目】如图1,△ABC中,AC=BC,∠A=30°,点D在AB边上,且∠ADC=45°.
(1)求∠BCD的度数;
(2)将图1中的△BCD绕点B顺时针旋转得到△BC′D′,当点D′恰好落在BC边上时,如图2所示,连接C′C并延长交AB于点E.
①求∠C′CB的度数;
②求证:△C′BD′≌△CAE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
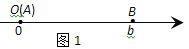

点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为∣AB∣.当A、B两点中有一点在原点时,不妨设点A在原点,如图1,∣AB∣=∣OB∣=∣b∣=∣a-b∣;当A、B两点都不在原点时,如图2,点A、B都在原点的右边∣AB∣=∣OB∣-∣OA∣=∣b∣-∣a∣=
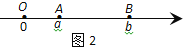
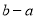 =∣a-b∣;如图3,当点A、B都在原点的左边,∣AB∣=∣OB∣-∣OA∣=∣b∣-∣a∣=
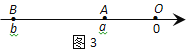
=∣a-b∣;如图3,当点A、B都在原点的左边,∣AB∣=∣OB∣-∣OA∣=∣b∣-∣a∣=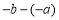 =∣a-b∣;如图4,当点A、B在原点的两边,∣AB∣=∣OB∣+∣OA∣=∣a∣+∣b∣=
=∣a-b∣;如图4,当点A、B在原点的两边,∣AB∣=∣OB∣+∣OA∣=∣a∣+∣b∣=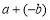 =∣a-b∣.
=∣a-b∣.回答下列问题:
(1)数轴上表示2和5的两点之间的距离是_____,数轴上表示1和-3的两点之间的距离是______.
(2)数轴上若点A表示的数是x,点B表示的数是-2,则点A和B之间的距离是_____,若∣AB∣=2,那么x为______.
(3)当x是_____时,代数式
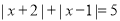 .
.(4)若点A表示的数是-1,点B与点A的距离是10,且点B在点A的右侧,动点P、Q同时从A、B出发沿数轴正方向运动,点P的速度是每秒3个单位长度,点Q的速度是每秒
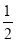 个单位长度,求运动几秒后,点P与点Q之间的距离为5个单位长度 ?(请写出必要的求解过程)
个单位长度,求运动几秒后,点P与点Q之间的距离为5个单位长度 ?(请写出必要的求解过程) -
科目: 来源: 题型:
查看答案和解析>>【题目】小林同学积极参加体育锻炼,天天坚持跑步,他每天以1000m为标准,超过的记作正数,不足的记作负数.下表是一周内小明跑步情况的记录(单位:m):
星期
一
二
三
四
五
六
日
跑步情况(m)
+420
+460
-100
-210
-330
+200
-240
(1)星期三小林跑了_____米
(2)小林在跑得最少的一天跑了______米?跑得最多的一天比最少的一天多跑了_____米?
(3)若小林跑步的平均速度为240米/分,求本周内小明用于跑步的时间.
相关试题

