搜索
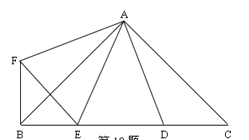
【题目】如图，∠BAC=∠DAF=90°，AB＝AC，AD＝AF，点D、E为BC边上的两点，且∠DAE＝45°，连接EF、BF，则下列结论：①△AED≌△AEF ②△AED为等腰三角形
③BE＋DC＞DE④BE2＋DC2=DE2，其中正确的有（ ）个
A. 4 B. 3 C. 2 D. 1
参考答案：
【答案】C
【解析】试题分析：：①∵∠DAF=90°，∠DAE=45°，∴∠FAE=∠DAF-∠DAE=45°．在△AED与△AEF中，AD=AF，∠DAE=∠FAE=45°，AE=AE，∴△AED≌△AEF（SAS），①正确；②∵∠BAC=90°，AB=AC，∴∠ABE=∠C=45°．∵点D、E为BC边上的两点，∠DAE=45°，∴AD与AE不一定相等，②错误；③∵∠BAC=∠DAF=90°，∴∠BAC-∠BAD=∠DAF-∠BAD，即∠CAD=∠BAF．在△ACD与△ABF中，AC=AB，∠CAD=∠BAF，AD=AF，∴△ACD≌△ABF（SAS），∴CD=BF，由①知△AED≌△AEF，∴DE=EF．在△BEF中，∵BE+BF＞EF，∴BE+DC＞DE，③正确；④由③知△ACD≌△ABF，∴∠C=∠ABF=45°，∵∠ABE=45°，∴∠EBF=∠ABE+∠ABF=90°．在Rt△BEF中，由勾股定理，得
，∵BF=DC，EF=DE，∴
，④正确．所以正确的结论有①③④．故选C．
-
科目： 来源： 题型：
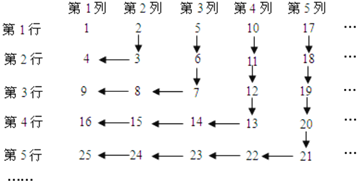
查看答案和解析>>【题目】（题文）正整数按图中的规律排列,请写出第18行,第20列的数字：_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】解方程：
(1)2x＋3＝x＋5;
(2)2(3y－1)－3(2－4y)＝9y＋10；
(3)
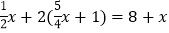
(4)
. -
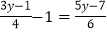科目： 来源： 题型：
查看答案和解析>>【题目】下列结论：
①若a＋b＋c＝0，且abc≠0，则
；②若a＋b＋c＝0，且a≠0，则x＝1一定是方程ax＋b＋c＝0的解；
③若a＋b＋c＝0，且abc≠0，则abc＞0；
④若|a|>|b|，则
>0.其中正确的结论是( )
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列说法：
①两点确定一条直线；
②两点之间，线段最短；
③若∠AOC＝
∠AOB，则射线OC是∠AOB的平分线；④连接两点之间的线段叫做这两点间的距离；
⑤学校在小明家南偏东25°方向上，则小明家在学校北偏西25°方向上.
其中正确的有________个．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，P，Q分别是BC，AC上的点，作PR⊥AB，PS⊥AC，垂足分别为R，S，若AQ＝PQ，PR＝PS，则这四个结论中正确的有( )
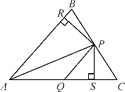
①PA平分∠BAC；②AS＝AR；③QP∥AR；④△BRP≌△CSP.
A. 4个 B. 3个 C. 2个 D. 1个
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知点O是直线AB上的一点，∠COE＝90°，OF是∠AOE的平分线．
(1)当点C，E，F在直线AB的同侧时(如图①所示)，试说明∠BOE＝2∠COF.
(2)当点C与点E，F在直线AB的两侧时(如图②所示)，(1)中的结论是否仍然成立？请给出你的结论，并说明理由．
相关试题
