Question

【题目】如图，正方形ABCD的边长为4，点G、H分别是BC、CD边上的点，直线GH与AB、AD的延长线相交于点E、F，连接AG、AH．

（1）当BG=2，DH=3时，则GH：HF=　　，∠AGH=　　°；

（2）若BG=3，DH=1，求DF、EG的长；

（3）设BG=x，DH=y，若△ABG∽△FDH，求y与x之间的函数关系式，并求出y的取值范围．

Answer 1

【答案】（1）1：3，90；（2）；（3）3≤y＜4．

【解析】试题分析：（1）根据正方形ABCD的边长为4，BG=2，DH=3，可得CG=2，CH=1，再根据DF∥CG，得出△FDH∽△GCH，根据相似三角形的性质可得GH：HF的值，最后根据勾股定理的逆定理，判定△AGH是直角三角形，且∠AGH=90°即可；

（2）根据正方形ABCD的边长为4，BG=3，DH=1，得出CG=1，CH=3，再根据CG∥DF，CH∥BE，可得△CGH∽△BGE∽△DFH，最后根据相似三角形的性质以及勾股定理，求得DF、EG的长；

（3）根据正方形ABCD的边长为4，BG=x，DH=y，得出CG=4﹣x，CH=4﹣y，由（1）可得，△FDH∽△GCH，而△ABG∽△FDH，进而得出△ABG∽△GCH，根据相似三角形的对应边成比例，可得y与x之间的函数关系式为：y=x2﹣x+4，最后运用二次函数的性质求得3≤y＜4即可．

试题解析：解：（1）∵正方形ABCD的边长为4，BG=2，DH=3，∴CG=2，CH=1，∵DF∥CG，∴△FDH∽△GCH，∴ ，∵Rt△GCH中，GH2=CG2+CH2=5，Rt△ABG中，AG2=AB2+BG2=20，Rt△ADH中，AH2=AD2+DH2=25，∴GH2+AG2=AH2，∴△AGH是直角三角形，且∠AGH=90°．

故答案为：1：3，90；

（2）∵正方形ABCD的边长为4，BG=3，DH=1，∴CG=1，CH=3，∵CG∥DF，CH∥BE，∴△CGH∽△BGE∽△DFH，∴ ，即 ，解得BE=9，DF=，∴Rt△BEG中，EG===；

（3）∵正方形ABCD的边长为4，BG=x，DH=y，∴CG=4﹣x，CH=4﹣y，由（1）可得，△FDH∽△GCH，而△ABG∽△FDH，∴△ABG∽△GCH，∴ ，即 ，∴y与x之间的函数关系式为：y=x2﹣x+4，∵，∴4﹣y= = ，∴当x=﹣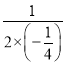 =2时，4﹣y有最大值，且最大值为﹣×4+2=1，∴0＜4﹣y≤1，解得3≤y＜4．