【题目】已知:在△ABC和△DCE中,∠ACB=∠DCE=90°,AC=DC,BC=EC,AB与DE相交于点F.
(1)如图1,求证AB=DE;
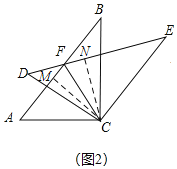
(2)如图2,连接CF,求证∠AFC=∠EFC;
(3)如图3,在(2)的条件下,当AF=EF时,连接BD,AE,延长CF交BD于点G,AE交CF于点H,若AE=8,BG=2,求线段GH的长.

参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)2.
【解析】
(1)证明△ABC≌△DEC(SAS),可得结论;
(2)如图2,作垂线段CM和CN,证明△ACM≌△DCN(AAS),得CM=CN,根据角平分线的逆定理可得:∠AFC=∠EFC;
(3)如图3,先证明△AFC≌△EFC,得AC=EC=BC,再证明△ACH≌△CBG(AAS),得CG和CH的长,利用线段的差可得结论.
证明:(1)如图1,在△ABC和△DEC中,
∵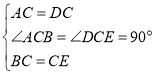 ,
,
∴△ABC≌△DEC(SAS),
∴AB=DE;
(2)如图2,过点C作CM⊥AB,CN⊥DE,垂足分别为M,N,
∵△ABC≌△DEC,
∴∠A=∠D,
在△ACM和△DCN中,
∵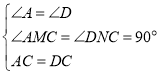 ,
,
∴△ACM≌△DCN(AAS),
∴CM=CN,
∴∠AFC=∠EFC;
(3)如图3,∵AB=DE,AF=EF,
∴AB-AF=DE-EF,即BF=DF,
∵∠AFC=∠EFC,∠AFC=∠BFG,∠EFC=∠DFG,
∴∠BFG=∠DFG,
∴FG⊥BD
∴∠BGF=∠DGF=90°,
同理∠AHF=∠EHF=90°,AH=EH=![]() AE=4,
AE=4,
在△AFC和△EFC中
∵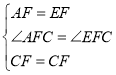
∴△AFC≌△EFC,
∴AC=EC,
∴AC=BC,
∵∠CBG+∠BCG=90°,∠ACH+∠BCG=90°,
∴∠CBG=∠ACH,
在△ACH和△CBG中,
∵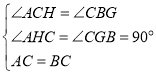 ,
,
∴△ACH≌△CBG(AAS),
∴CH=BG=2,CG=AH=4,
∴GH=CG-CH=4-2=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为4,点G、H分别是BC、CD边上的点,直线GH与AB、AD的延长线相交于点E、F,连接AG、AH.
(1)当BG=2,DH=3时,则GH:HF= ,∠AGH= °;
(2)若BG=3,DH=1,求DF、EG的长;
(3)设BG=x,DH=y,若△ABG∽△FDH,求y与x之间的函数关系式,并求出y的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】光明电器超市销售每台进价分别为190元、160元的A、B两种型号的电风扇,下表是近两周的销售情况:
销售时段
销售数量
销售收入
A种型号
B种型号
第一周
2台
6台
1840元
第二周
5台
7台
2840 元
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备再采购这两种型号的电风扇共40台,这40台电风扇全部售出后,若利润不低于2660元,求A种型号的电风扇至少要采购多少台?
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:

(1)作出△ABC绕点A逆时针旋转90°的△A1B1C1;作出△ABC关于原点O成中心对称的△A2B2C2;
(2)点B1的坐标为__________,点C2的坐标为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O1、O2、室O3,…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒
 个单位长度,则第2018秒时,点P的坐标是( )
个单位长度,则第2018秒时,点P的坐标是( )
A. (2017,0)B. (2018,﹣1)C. (2017,1)D. (2018,0)
-
科目: 来源: 题型:
查看答案和解析>>【题目】填空并完成推理过程.
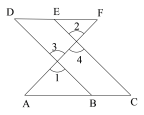
如图,E点为DF上的点,B点为AC上的点,∠1=∠2,∠C=∠D,试说明:AC∥DF.
证明:∵∠1=∠2(已知)
∠1=∠3(对顶角相等)
∴∠2=∠3( )
∴____∥______( )
∴∠C=∠ABD( )
又∵∠C=∠D(已知)
∴∠D=∠ABD(等量代换)
∴AC∥DF( )
-
科目: 来源: 题型:
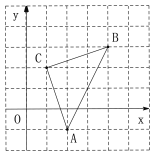
查看答案和解析>>【题目】如图,直角坐标系中,三角形ABC的顶点都在网格点上,其中A(2,
 ), B(4,3), C(1,2).
), B(4,3), C(1,2).(1)将三角形ABC先向左平移2个单位长度,再向上平移1个单位长度,得到三角形
 ,则三角形
,则三角形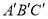 的三个顶点坐标。
的三个顶点坐标。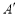 ( ),
( ),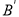 ( ),
( ),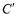 ( ).
( ).(2)求三角形ABC的面积.
相关试题

