【题目】用棋子摆成的“上”字型图案如图所示现察此图案的规律,并回答:
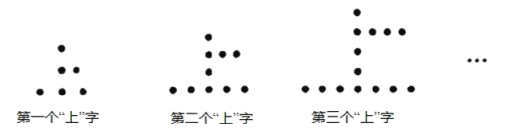
(1)依照此规律,第五个图形中共有 个棋子,第八个图形中共有 个棋子.
(2)第![]() (
(![]() 为正整数)个图形中共有 个棋子.
为正整数)个图形中共有 个棋子.
(3)根据(2)中的结论,第几个图形中有2022个棋子?
参考答案:
【答案】(1)22,34;(2)![]() ;(3)第505个图形中有2022个棋子
;(3)第505个图形中有2022个棋子
【解析】
(1)根据图形可以写出前几个图形中棋子的个数,从而发现棋子的变化规律,从而可以得到第五个和第八个图形中的棋子个数;
(2)根据(1)中发现的规律,可以得到第n(n为正整数)个图形中棋子的个数;
(3)根据(2)中的结果,可以求得第几个图形中有2022个棋子.
(1)由图可得:
第一图形中的“上”字中棋子的个数为:3×2=6,
第二图形中的“上”字中棋子的个数为:5×2=10,
第三图形中的“上”字中棋子的个数为:7×2=14,
…,
则第五个图形中共有:(2×5+1)×2=22(个),
第八个图形中共有:(2×8+1)×2=34(个).
故答案为:22,34;
(2)第n(n为正整数)个图形中共有:(2n+1)×2=(4n+2)(个).
故答案为:(4n+2);
(3)令4n+2=2022,
解得:n=505,
即第505个图形中有2022个棋子.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等腰直角三角形
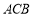 的边
的边 ,等腰直角三角形
,等腰直角三角形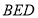 的边
的边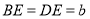 ,且
,且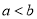 ,点
,点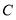 、
、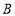 、
、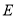 放置在一条直线上,联结
放置在一条直线上,联结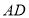 .
.(1)求三角形
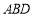 的面积;
的面积;(2)如果点
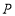 是线段
是线段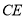 的中点,联结
的中点,联结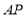 、
、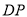 得到三角形
得到三角形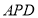 ,求三角形
,求三角形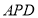 的面积;
的面积;(3)第(2)小题中的三角形
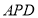 与三角形
与三角形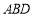 面积哪个较大?大多少?(结果都可用
面积哪个较大?大多少?(结果都可用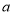 、
、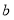 代数式表示,并化简)
代数式表示,并化简)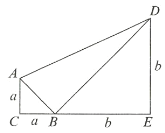
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
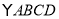 中,
中, ,
, 是对角线
是对角线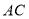 上不同的两点,下列条件中,不能得出四边形
上不同的两点,下列条件中,不能得出四边形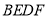 一定为平行四边形的是( )
一定为平行四边形的是( )A.
 B.
B.  C.
C. 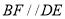 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,点O是坐标原点,四边形ABCO是菱形,点A的坐标为(﹣3,4),点C在x轴的正半轴上,直线AC交y轴于点M,AB边交y轴于点H,连接BM.
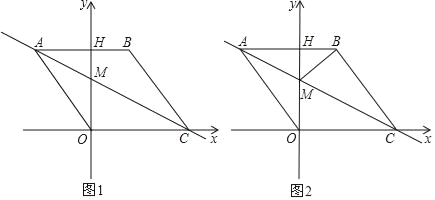
(1)菱形ABCO的边长
(2)求直线AC的解析式;
(3)动点P从点A出发,沿折线ABC方向以2个单位/秒的速度向终点C匀速运动,设△PMB的面积为S(S≠0),点P的运动时间为t秒,
①当0<t<
 时,求S与t之间的函数关系式;
时,求S与t之间的函数关系式;②在点P运动过程中,当S=3,请直接写出t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,AB为直径,且AB⊥CD,垂足为E,CD=
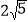 ,AE=5.
,AE=5.(1)求⊙O半径r的值;
(2)点F在直径AB上,连结CF,当∠FCD=
 ∠DOB时,直接写出EF的长,并在图中标出F点的具体位置.
∠DOB时,直接写出EF的长,并在图中标出F点的具体位置.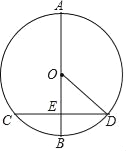
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.

(1)根据图示填写下表;
平均数(分)
中位数(分)
众数(分)
初中部
85
高中部
85
100
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O分别与BC、AC交于点D、E,过点D作⊙O的切线DF,交AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.

相关试题

