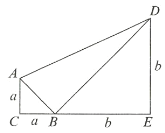
【题目】如图,已知等腰直角三角形![]() 的边
的边![]() ,等腰直角三角形
,等腰直角三角形![]() 的边
的边![]() ,且
,且![]() ,点
,点![]() 、
、![]() 、
、![]() 放置在一条直线上,联结
放置在一条直线上,联结![]() .
.
(1)求三角形![]() 的面积;
的面积;
(2)如果点![]() 是线段
是线段![]() 的中点,联结
的中点,联结![]() 、
、![]() 得到三角形
得到三角形![]() ,求三角形
,求三角形![]() 的面积;
的面积;
(3)第(2)小题中的三角形![]() 与三角形
与三角形![]() 面积哪个较大?大多少?(结果都可用
面积哪个较大?大多少?(结果都可用![]() 、
、![]() 代数式表示,并化简)
代数式表示,并化简)
参考答案:
【答案】(1)![]() (2)
(2)![]() (3)三角形
(3)三角形![]() 的面积比三角形
的面积比三角形![]() 的面积大,大
的面积大,大![]() .
.
【解析】
(1)由题意知![]() (同旁内角互补,两条直线平行),所以四边形
(同旁内角互补,两条直线平行),所以四边形![]() 是梯形,再由梯形面积减去两个等腰直角三角形面积即可求得;
是梯形,再由梯形面积减去两个等腰直角三角形面积即可求得;
(2)与题(1)思路完全一样,由梯形面积减去两个直角三角形面积即可求得;
(3)将所求的两个面积作差,化简并与0比较大小即可.
(1)![]()
(2)![]()
(3)![]() ,∵
,∵![]() ,∴
,∴![]() ,即三角形
,即三角形![]() 的面积比三角形
的面积比三角形![]() 的面积大,大
的面积大,大![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
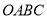 的两条边
的两条边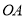 、
、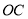 分别在
分别在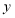 轴和
轴和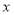 轴上,已知点
轴上,已知点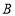 坐标为(4,–3).把矩形
坐标为(4,–3).把矩形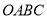 沿直线
沿直线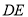 折叠,使点
折叠,使点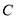 落在点
落在点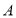 处,直线
处,直线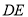 与
与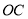 、
、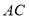 、
、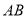 的交点分别为
的交点分别为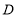 、
、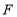 、
、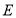 .
.(1)线段
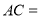 ;
;(2)求点
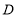 坐标及折痕
坐标及折痕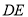 的长;
的长;(3)若点
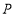 在
在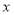 轴上,在平面内是否存在点
轴上,在平面内是否存在点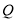 ,使以
,使以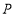 、
、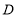 、
、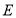 、
、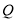 为顶点的四边形是菱形?若存在,则请求出点
为顶点的四边形是菱形?若存在,则请求出点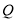 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;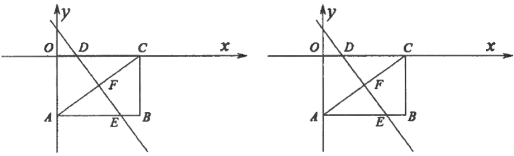
-
科目: 来源: 题型:
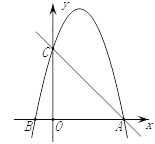
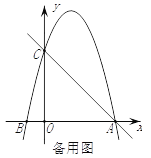
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点C(0,4),点A、B在x轴上,并且OA=OC=4OB,动点P在过A、B、C三点的抛物线上.
(1)求抛物线的函数表达式;
(2)在直线AC上方的抛物线上,是否存在点P,使得△PAC的面积最大?若存在,求出P点坐标及ΔPAC面积的最大值;若不存在,请说明理由.
(3)在x轴上是否存在点Q,使得△ACQ是等腰三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个圆柱体包装盒,高40cm,底面周长20cm.现将彩色矩形纸带AMCN裁剪成一个平行四边形ABCD(如图1),然后用这条平行四边形纸带按如图2的方式把这个圆柱体包装盒的侧面进行包贴(要求包贴时没有重叠部分),纸带在侧面缠绕四圈,正好将这个圆柱体包装盒的侧面全部包贴满,则所需的纸带AD的长度为_____ cm.
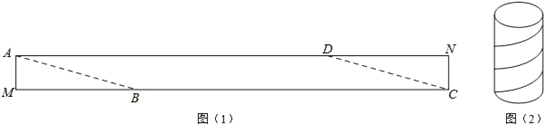
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
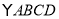 中,
中, ,
, 是对角线
是对角线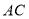 上不同的两点,下列条件中,不能得出四边形
上不同的两点,下列条件中,不能得出四边形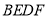 一定为平行四边形的是( )
一定为平行四边形的是( )A.
 B.
B.  C.
C. 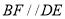 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,点O是坐标原点,四边形ABCO是菱形,点A的坐标为(﹣3,4),点C在x轴的正半轴上,直线AC交y轴于点M,AB边交y轴于点H,连接BM.
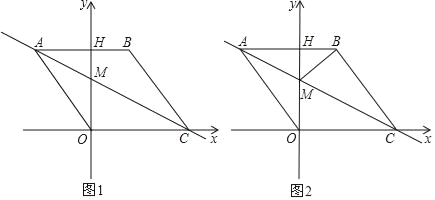
(1)菱形ABCO的边长
(2)求直线AC的解析式;
(3)动点P从点A出发,沿折线ABC方向以2个单位/秒的速度向终点C匀速运动,设△PMB的面积为S(S≠0),点P的运动时间为t秒,
①当0<t<
 时,求S与t之间的函数关系式;
时,求S与t之间的函数关系式;②在点P运动过程中,当S=3,请直接写出t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用棋子摆成的“上”字型图案如图所示现察此图案的规律,并回答:
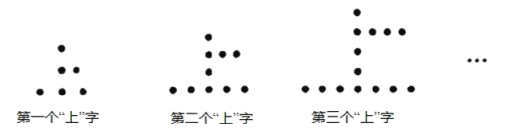
(1)依照此规律,第五个图形中共有 个棋子,第八个图形中共有 个棋子.
(2)第
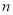 (
(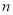 为正整数)个图形中共有 个棋子.
为正整数)个图形中共有 个棋子.(3)根据(2)中的结论,第几个图形中有2022个棋子?
相关试题

