【题目】函数f(x)=ex(﹣x2+2x+a)在区间[a,a+1]上单调递增,则实数a的最大值为 .
参考答案:
【答案】![]()
【解析】解:f(x)=ex(﹣x2+2x+a), f′(x)=ex(﹣x2+a+2),
若f(x)在[a,a+1]上单调递增,
则﹣x2+a+2≥0在[a,a+1]恒成立,
即a+2≥x2在[a,a+1]恒成立,
①a+1<0即a<﹣1时,y=x2在[a,a+1]递减,
y=x2的最大值是y=a2 ,
故a+2≥a2 , 解得:a2﹣a﹣2≤0,解得:﹣1<a<2,不合题意,舍;
②﹣1≤a≤0时,y=x2在[a,0)递减,在(0,a+1]递增,
故y=x2的最大值是a2或(a+1)2 ,
③a>0时,y=x2在[a,a+1]递增,y的最大值是(a+1)2 ,
故a+2≥(a+1)2 , 解得:0<a≤ ![]() ,
,
则实数a的最大值为: ![]() ,
,
综上,a的最大值是 ![]() ,
,
所以答案是: ![]() .
.
【考点精析】认真审题,首先需要了解利用导数研究函数的单调性(一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减).
在这个区间单调递减).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,Rt△PAB的直角顶点P(3,4)在函数y=
 (x>0)的图象上,顶点A、B在函数y=
(x>0)的图象上,顶点A、B在函数y=  (x>0,0<t<k)的图象上,PA∥x轴,连接OP,OA,记△OPA的面积为S△OPA , △PAB的面积为S△PAB , 设w=S△OPA﹣S△PAB . ①求k的值以及w关于t的表达式;
(x>0,0<t<k)的图象上,PA∥x轴,连接OP,OA,记△OPA的面积为S△OPA , △PAB的面积为S△PAB , 设w=S△OPA﹣S△PAB . ①求k的值以及w关于t的表达式;
②若用wmax和wmin分别表示函数w的最大值和最小值,令T=wmax+a2﹣a,其中a为实数,求Tmin .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图示AB为⊙O的一条弦,点C为劣弧AB的中点,E为优弧AB上一点,点F在AE的延长线上,且BE=EF,线段CE交弦AB于点D.
①求证:CE∥BF;
②若BD=2,且EA:EB:EC=3:1: ,求△BCD的面积(注:根据圆的对称性可知OC⊥AB).
,求△BCD的面积(注:根据圆的对称性可知OC⊥AB).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=﹣x2+bx+c+1,
①当b=1时,求这个二次函数的对称轴的方程;
②若c= b2﹣2b,问:b为何值时,二次函数的图象与x轴相切?
b2﹣2b,问:b为何值时,二次函数的图象与x轴相切?
③若二次函数的图象与x轴交于点A(x1 , 0),B(x2 , 0),且x1<x2 , 与y轴的正半轴交于点M,以AB为直径的半圆恰好过点M,二次函数的对称轴l与x轴、直线BM、直线AM分别交于点D、E、F,且满足 =
=  ,求二次函数的表达式.
,求二次函数的表达式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b,c为正实数,且
 ,则
,则  的取值范围为 .
的取值范围为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥A﹣BCD中,E,F分别为BC,CD上的点,且BD∥平面AEF.

(1)求证:EF∥平ABD面;
(2)若AE⊥平面BCD,BD⊥CD,求证:平面AEF⊥平面ACD. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
 为实数.
为实数.
(1)若 ,求t的值;
,求t的值;
(2)若t=1,且 ,求
,求 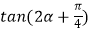 的值.
的值.
相关试题

