【题目】如图示AB为⊙O的一条弦,点C为劣弧AB的中点,E为优弧AB上一点,点F在AE的延长线上,且BE=EF,线段CE交弦AB于点D.
①求证:CE∥BF;
②若BD=2,且EA:EB:EC=3:1: ![]() ,求△BCD的面积(注:根据圆的对称性可知OC⊥AB).
,求△BCD的面积(注:根据圆的对称性可知OC⊥AB).
参考答案:
【答案】①证明:连接AC,BE,作直线OC,如图所示: 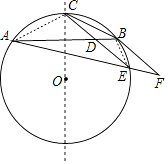
∵BE=EF,
∴∠F=∠EBF;
∵∠AEB=∠EBF+∠F,
∴∠F= ![]() ∠AEB,
∠AEB,
∵C是 ![]() 的中点,∴
的中点,∴ ![]() ,
,
∴∠AEC=∠BEC,
∵∠AEB=∠AEC+∠BEC,
∴∠AEC= ![]() ∠AEB,
∠AEB,
∴∠AEC=∠F,
∴CE∥BF;
②解:∵∠DAE=∠DCB,∠AED=∠CEB,
∴△ADE∽△CBE,
∴ ![]() ,即
,即 ![]() ,
,
∵∠CBD=∠CEB,∠BCD=∠ECB,
∴△CBE∽△CDB,
∴ ![]() ,即
,即 ![]() ,
,
∴CB=2 ![]() ,
,
∴AD=6,
∴AB=8,
∵点C为劣弧AB的中点,
∴OC⊥AB,AG=BG= ![]() AB=4,
AB=4,
∴CG= ![]() =2,
=2,
∴△BCD的面积= ![]() BDCG=
BDCG= ![]() ×2×2=2.
×2×2=2.
【解析】①连接AC,BE,由等腰三角形的性质和三角形的外角性质得出∠F= ![]() ∠AEB,由圆周角定理得出∠AEC=∠BEC,证出∠AEC=∠F,即可得出结论;②证明△ADE∽△CBE,得出
∠AEB,由圆周角定理得出∠AEC=∠BEC,证出∠AEC=∠F,即可得出结论;②证明△ADE∽△CBE,得出 ![]() ,证明△CBE∽△CDB,得出
,证明△CBE∽△CDB,得出 ![]() ,求出CB=2
,求出CB=2 ![]() ,得出AD=6,AB=8,由垂径定理得出OC⊥AB,AG=BG=
,得出AD=6,AB=8,由垂径定理得出OC⊥AB,AG=BG= ![]() AB=4,由勾股定理求出CG=
AB=4,由勾股定理求出CG= ![]() =2,即可得出△BCD的面积.
=2,即可得出△BCD的面积.
【考点精析】解答此题的关键在于理解垂径定理的相关知识,掌握垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧,以及对相似三角形的判定与性质的理解,了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图示,正方形ABCD的顶点A在等腰直角三角形DEF的斜边EF上,EF与BC相交于点G,连接CF.
①求证:△DAE≌△DCF;
②求证:△ABG∽△CFG.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图示一架水平飞行的无人机AB的尾端点A测得正前方的桥的左端点P的俯角为α其中tanα=2
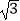 ,无人机的飞行高度AH为500
,无人机的飞行高度AH为500 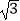 米,桥的长度为1255米.
米,桥的长度为1255米.
①求点H到桥左端点P的距离;
②若无人机前端点B测得正前方的桥的右端点Q的俯角为30°,求这架无人机的长度AB.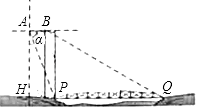
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,Rt△PAB的直角顶点P(3,4)在函数y=
 (x>0)的图象上,顶点A、B在函数y=
(x>0)的图象上,顶点A、B在函数y=  (x>0,0<t<k)的图象上,PA∥x轴,连接OP,OA,记△OPA的面积为S△OPA , △PAB的面积为S△PAB , 设w=S△OPA﹣S△PAB . ①求k的值以及w关于t的表达式;
(x>0,0<t<k)的图象上,PA∥x轴,连接OP,OA,记△OPA的面积为S△OPA , △PAB的面积为S△PAB , 设w=S△OPA﹣S△PAB . ①求k的值以及w关于t的表达式;
②若用wmax和wmin分别表示函数w的最大值和最小值,令T=wmax+a2﹣a,其中a为实数,求Tmin .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=﹣x2+bx+c+1,
①当b=1时,求这个二次函数的对称轴的方程;
②若c= b2﹣2b,问:b为何值时,二次函数的图象与x轴相切?
b2﹣2b,问:b为何值时,二次函数的图象与x轴相切?
③若二次函数的图象与x轴交于点A(x1 , 0),B(x2 , 0),且x1<x2 , 与y轴的正半轴交于点M,以AB为直径的半圆恰好过点M,二次函数的对称轴l与x轴、直线BM、直线AM分别交于点D、E、F,且满足 =
=  ,求二次函数的表达式.
,求二次函数的表达式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=ex(﹣x2+2x+a)在区间[a,a+1]上单调递增,则实数a的最大值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b,c为正实数,且
 ,则
,则  的取值范围为 .
的取值范围为 .
相关试题

