【题目】已知a,b,c为正实数,且 ![]() ,则
,则 ![]() 的取值范围为 .
的取值范围为 .
参考答案:
【答案】[27,30]
【解析】解:∵ ![]() , ∴
, ∴ 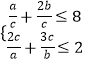 ,设x=
,设x= ![]() ,y=
,y= ![]() ,则有
,则有 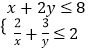 ,
,
∴ 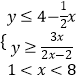 ,
,
作出平面区域如图所示: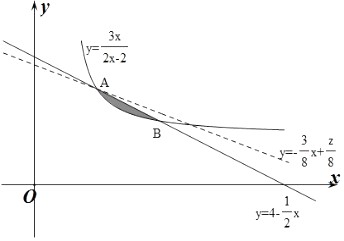
令z= ![]() =3x+8y,则y=﹣
=3x+8y,则y=﹣ ![]() +
+ ![]() ,
,
由图象可知当直线y=﹣ ![]() +
+ ![]() 经过点A时,截距最大,即z最大;
经过点A时,截距最大,即z最大;
当直线y=﹣ ![]() +
+ ![]() 与曲线y=
与曲线y= ![]() 相切时,截距最小,即z最小.
相切时,截距最小,即z最小.
解方程组  得A(2,3),∴z的最大值为3×2+8×3=30,
得A(2,3),∴z的最大值为3×2+8×3=30,
设直线y=﹣ ![]() +
+ ![]() 与曲线y=
与曲线y= ![]() 的切点为(x0 , y0),
的切点为(x0 , y0),
则( ![]() )′|
)′| ![]() =﹣
=﹣ ![]() ,即
,即 ![]() =﹣
=﹣ ![]() ,解得x0=3,
,解得x0=3,
∴切点坐标为(3, ![]() ),∴z的最小值为3×3+8×
),∴z的最小值为3×3+8× ![]() =27.
=27.
∴27≤z≤30,
所以答案是:[27,30].
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图示AB为⊙O的一条弦,点C为劣弧AB的中点,E为优弧AB上一点,点F在AE的延长线上,且BE=EF,线段CE交弦AB于点D.
①求证:CE∥BF;
②若BD=2,且EA:EB:EC=3:1: ,求△BCD的面积(注:根据圆的对称性可知OC⊥AB).
,求△BCD的面积(注:根据圆的对称性可知OC⊥AB).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=﹣x2+bx+c+1,
①当b=1时,求这个二次函数的对称轴的方程;
②若c= b2﹣2b,问:b为何值时,二次函数的图象与x轴相切?
b2﹣2b,问:b为何值时,二次函数的图象与x轴相切?
③若二次函数的图象与x轴交于点A(x1 , 0),B(x2 , 0),且x1<x2 , 与y轴的正半轴交于点M,以AB为直径的半圆恰好过点M,二次函数的对称轴l与x轴、直线BM、直线AM分别交于点D、E、F,且满足 =
=  ,求二次函数的表达式.
,求二次函数的表达式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=ex(﹣x2+2x+a)在区间[a,a+1]上单调递增,则实数a的最大值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥A﹣BCD中,E,F分别为BC,CD上的点,且BD∥平面AEF.

(1)求证:EF∥平ABD面;
(2)若AE⊥平面BCD,BD⊥CD,求证:平面AEF⊥平面ACD. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
 为实数.
为实数.
(1)若 ,求t的值;
,求t的值;
(2)若t=1,且 ,求
,求 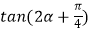 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在水域上建一个演艺广场,演艺广场由看台Ⅰ,看台Ⅱ,三角形水域ABC,及矩形表演台BCDE四个部分构成(如图),看台Ⅰ,看台Ⅱ是分别以AB,AC为直径的两个半圆形区域,且看台Ⅰ的面积是看台Ⅱ的面积的3倍,矩形表演台BCDE 中,CD=10米,三角形水域ABC的面积为
 平方米,设∠BAC=θ.
平方米,设∠BAC=θ. 
(1)求BC的长(用含θ的式子表示);
(2)若表演台每平方米的造价为0.3万元,求表演台的最低造价.
相关试题

