【题目】如图,在△ABC中,∠A=m°,∠ABC和∠ACD的平分线相交于点A1,得∠A1;∠A1BC和∠A1CD的平分线相交于点A2,得∠A2;…;∠A2018BC和∠A2018CD的平分线交于点A2019,则∠A2019=________度.

参考答案:
【答案】![]()
【解析】
根据角平分线的定义可得∠A1BC=![]() ∠ABC,∠A1CD=
∠ABC,∠A1CD=![]() ∠ACD,再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ACD=∠A+∠ABC,∠A1CD=∠A1+∠A1BC,然后整理得到∠A1=
∠ACD,再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ACD=∠A+∠ABC,∠A1CD=∠A1+∠A1BC,然后整理得到∠A1=![]() ∠A;
∠A;
∵∠ABC与∠ACD的平分线交于点A1,
∴∠A1BC=![]() ∠ABC,∠A1CD=
∠ABC,∠A1CD=![]() ∠ACD,
∠ACD,
由三角形的外角性质,∠ACD=∠A+∠ABC,
∠A1CD=∠A1+∠A1BC,![]() (∠A+∠ABC)=∠A1+∠A1BC=∠A1+
(∠A+∠ABC)=∠A1+∠A1BC=∠A1+![]() ∠ABC,
∠ABC,
整理得,∠A1=![]() ∠A=
∠A=![]() ×m°=
×m°=![]() °;
°;
同理可得∠An=(![]() )n×m,
)n×m,
所以∠A2019=(![]() )2019×m=
)2019×m=![]() .
.
故答案是:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】周末,老师带同学去北京植物园中的一二﹒九运动纪念广场,这里有三座侧面为三角形的纪念亭,挺拔的建筑线条象征青年朝气蓬勃、积极向上的精神.基于纪念亭的几何特征,同学们编拟了如下的数学问题:

如图1,点A,B,C,D在同一条直线上,在四个论断“EA=ED,EF⊥AD,AB=DC,FB=FC”中选择三个作为已知条件,另一个作为结论,构成真命题(补充已知和求证),并进行证明.
已知:如图,点A,B,C,D在同一条直线上, .
求证: .
证明: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B=40°,∠C=60°,AD⊥BC于D,AE是∠BAC的平分线.

(1)求∠DAE的度数;
(2)写出以AD为高的所有三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程m1x2+
 x+1=0的两根分别为x1 , x2 , 一元二次方程m2x2+
x+1=0的两根分别为x1 , x2 , 一元二次方程m2x2+  x+1=0的两根为x3 , x4 , 若x1<x3<x4<x2<0,则m1 , m2的大小关系为( )
x+1=0的两根为x3 , x4 , 若x1<x3<x4<x2<0,则m1 , m2的大小关系为( )
A.0>m1>m2
B.0>m2>m1
C.m2>m1>0
D.m1>m2>0 -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
在学习“可化为一元一次方程的分式方程及其解法”的过程中,老师提出一个问题:若关于x的分式方程
 =1的解为正数,求a的取值范围.
=1的解为正数,求a的取值范围.经过独立思考与分析后,小杰和小哲开始交流解题思路如下:
小杰说:解这个关于x的分式方程,得x=a+4.由题意可得a+4>0,所以a>﹣4,问题解决.
小哲说:你考虑的不全面,还必须保证x≠4,即a+4≠4才行.
(1)请回答: 的说法是正确的,并简述正确的理由是 ;
(2)参考对上述问题的讨论,解决下面的问题:
若关于x的方程
 的解为非负数,求m的取值范围.
的解为非负数,求m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+1(k≠0)与反比例函数y=
 (m≠0)的图象有公共点A(1,2).直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别交于点B,C.
(m≠0)的图象有公共点A(1,2).直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别交于点B,C. 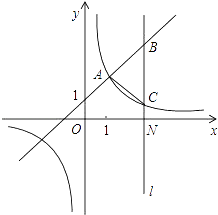
(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积? -
科目: 来源: 题型:
查看答案和解析>>【题目】用两种方法证明“三角形的外角和等于360°”.
已知:如图,∠BAE,∠CBF,∠ACD是△ABC的三个外角.
求证:∠BAE+∠CBF+∠ACD=360°.
证法1:∵________________________________________________________________,
∴∠BAE+∠1+∠CBF+∠2+∠ACD+∠3=180°×3=540°,
∴∠BAE+∠CBF+∠ACD=540°-(∠1+∠2+∠3).
∵______________,
∴∠BAE+∠CBF+∠ACD=540°-180°=360°.
请把证法1补充完整,并用不同的方法完成证法2.

相关试题

