【题目】周末，老师带同学去北京植物园中的一二﹒九运动纪念广场，这里有三座侧面为三角形的纪念亭，挺拔的建筑线条象征青年朝气蓬勃、积极向上的精神．基于纪念亭的几何特征，同学们编拟了如下的数学问题：
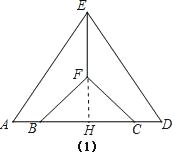
如图1，点A，B，C，D在同一条直线上，在四个论断“EA=ED，EF⊥AD，AB=DC，FB=FC”中选择三个作为已知条件，另一个作为结论，构成真命题（补充已知和求证），并进行证明．
已知：如图，点A，B，C，D在同一条直线上， ．
求证： ．
证明： ．
小学生10分钟口算测试100分系列答案科目：初中数学 来源： 题型：
【题目】在⊙O中，弦AB、CD相交于点E，连接AC、BC，AC=BC，AB=CD． 
（1）如图1，求证：BE平分∠CBD；
（2）如图2，F为BC上一点，连接AF交CD于点G，当∠FAB= 
∠ACB时，求证：AC=BD+2CF；
（3）如图3，在（2）的条件下，若S△ACF=S△CBD ， ⊙O的半径为3 
，求线段GD的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列说法：
①要了解一批灯泡的使用寿命，应采用普查的方式；
②若一个游戏的中奖率是1%，则做100次这样的游戏一定会中奖；
③甲、乙两组数据的样本容量与平均数分别相同，若方差 
=0.1， 
=0.2，则甲组数据比乙组数据稳定；
④“掷一枚硬币，正面朝上”是必然事件．
正确说法的序号是（ ）
A.①
B.②
C.③
D.④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，△ABC是等边三角形，点D为AB上一点，现将△ABC沿EF折叠，使得顶点A与D点重合，且FD⊥BC，则 
的值等于（ ） 
A.
B.
C.
D.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，一次函数y=kx+1（k≠0）与反比例函数y= 
（m≠0）的图象有公共点A（1，2）．直线l⊥x轴于点N（3，0），与一次函数和反比例函数的图象分别交于点B，C． 
（1）求一次函数与反比例函数的解析式；
（2）求△ABC的面积？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某学校的校门是伸缩门（如图1），伸缩门中的每一行菱形有20个，每个菱形边长为30厘米．校门关闭时，每个菱形的锐角度数为60°（如图2）；校门打开时，每个菱形的锐角度数从60°缩小为10°（如图3）．问：校门打开了多少米？（结果精确到1米，参考数据：sin5°≈0.0872，cos5°≈0.9962，sin10°≈0.1736，cos10°≈0.9848）． 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，将坐标为(0，0)，(2，1)，(2，4)，(0，3)的点依次连结起来形成一个图案.
(1)这四个点的横坐标保持不变，纵坐标变成原来的
，将所有的四个点用线段依次连结起来，所得的图案与原图案相比有什么变化?
(2)纵、横坐标分别变成原来的2倍呢？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】杭州市某4所高中近两年的最低录取分数线如下表（单位：分），设4所高中2011年和2012年的平均最低录取分数线分别为 
， 
，则 
=分 杭州市某4所高中最低录取分数线统计表
学校 | 2011年 | 2012年 |
杭州A中 | 438 | 442 |
杭州B中 | 435 | 442 |
杭州C中 | 435 | 439 |
杭州D中 | 435 | 439 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
