Question

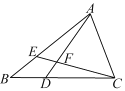
【题目】如图，在△ABC中，点E在AB上，点D在BC上，BD＝BE，∠BAD＝∠BCE，AD与CE相交于点F，试判断△AFC的形状，并说明理由．

Answer 1

【答案】△AFC是等腰三角形．理由见解析．

【解析】

试题根据条件证明△BAD≌△BCE从而得出BA=BC，∠BAD=∠BCE，然后结合条件证明∠FAC=∠FCA即可．

试题解析：△AFC是等腰三角形．理由如下：

在△BAD与△BCE中，

∵∠B=∠B（公共角），∠BAD=∠BCE，BD=BE，

∴△BAD≌△BCE（AAS），

∴BA=BC，∠BAD=∠BCE，

∴∠BAC=∠BCA，

∴∠BAC﹣∠BAD=∠BCA﹣∠BCE，即∠FAC=∠FCA．

∴AF=CF，

∴△AFC是等腰三角形．