【题目】某网店3月份经营一种热销商品,每件成本20元,发现三周内售价在持续提升,销售单价P(元/件)与时间t(天)之间的函数关系为P=30+ ![]() t(其中1≤t≤21,t为整数),且其日销售量y(件)与时间t(天)的关系如下表
t(其中1≤t≤21,t为整数),且其日销售量y(件)与时间t(天)的关系如下表
时间t(天) | 1 | 5 | 9 | 13 | 17 | 21 |
日销售量y(件) | 118 | 110 | 102 | 94 | 86 | 78 |
(1)已知y与t之间的变化规律符合一次函数关系,请直接写出y(件)与时间t(天)函数关系式;
(2)在这三周的销售中,第几天的销售利润最大?最大日销售利润为多少?
(3)在实际销售的21天中,该网店每销售一件商品就捐赠a元利润(a<8)给“精准扶贫”的对象,通过销售记录发现,这21天中,每天扣除捐赠后的日销售利润随时间t(天)的增大而增大,求a的取值范围.
参考答案:
【答案】
(1)解:设y(件)与时间t(天)函数关系式是y=kt+b,
![]() ,得
,得 ![]() ,
,
即y(件)与时间t(天)函数关系式是y=﹣2t+120;
(2)解:设日销售利润为w元,
w=(30+ ![]() t﹣20)(﹣2t+120)=
t﹣20)(﹣2t+120)= ![]() ,
,
∴当t=10时,w取得最大值,此时w=1250,
答:第10天的销售利润最大,最大利润是1250元;
(3)解:设捐赠后的每日的销售利润为w1元,
w1=(30+ ![]() t﹣20﹣a)(﹣2t+120)=
t﹣20﹣a)(﹣2t+120)= ![]() ,
,
∴w1的对称轴是t= 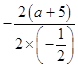 =2a+10,
=2a+10,
∵这21天中,每天扣除捐赠后的日销售利润随时间t(天)的增大而增大,
∴2a+10≥21,
解得,a≥5.5,
又∵a<8,
∴5.5≤a<8,
即a的取值范围是5.5≤a<8.
【解析】(1)根据题意可以设出y(件)与时间t(天)函数关系式,然后根据表格中的数据即可解答本题;(2)根据题意可以得到利润与t的函数关系式,然后化为顶点式即可解答本题;(3)根据题意可以得到相应的函数解析式,然后根据二次函数的性质即可解答本题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,C、G是⊙O上两点,且AC=CG,过点C的直线CD⊥BG于点D,交BA的延长线于点E,连接BC,交OD于点F.
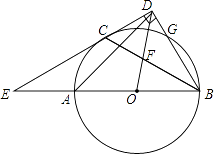
(1)求证:CD是⊙O的切线.
(2)若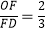 ,求∠E的度数.
,求∠E的度数.
(3)连接AD,在(2)的条件下,若CD=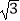 ,求AD的长.
,求AD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,网格图中小方格都是边长为1个单位长度的小正方形,已知三角形ABC的三个顶点都在网格的格点上,按要求完成下列各小题.
(1)请在图中画出将三角形ABC先向上平移1个单位长度,再向右平移3个单位长度后的图形,即三角形A′B′C′,并指出图中相等的线段;
(2)在(1)的基础上,A′B′,B′C′分别与AC交于点E,F.若∠A=50°,∠C′=51°,分别求出∠A′EF与∠B′FC的度数.
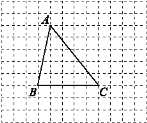
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,∠ABD和∠BDC的平分线交于点E,BE交CD于点F,∠1+∠2=90°.
(1)试说明:AB∥CD;
(2)试探究∠2与∠3的数量关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.

(1)求证:四边形DEFG是平行四边形;
(2)若M为EF的中点,OM=3,∠OBC和∠OCB互余,求DG的长度.
-
科目: 来源: 题型:
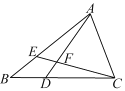
查看答案和解析>>【题目】如图,在△ABC中,点E在AB上,点D在BC上,BD=BE,∠BAD=∠BCE,AD与CE相交于点F,试判断△AFC的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是由一些大小相同的小正方体组合成的简单几何体.根据要求完成下列题目.
(1)正面图中有______块小正方体;
(2)请在下面方格纸中分别画出它的左视图和俯视图(画出的图都用铅笔涂上阴影)
(3)用小正方体搭一个几何体,使得它的左视图和俯视图与你在(2)中所画的图一致,则这样的几何体最多要______块小正方体.

相关试题

