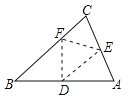
【题目】如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.

(1)求证:四边形DEFG是平行四边形;
(2)若M为EF的中点,OM=3,∠OBC和∠OCB互余,求DG的长度.
参考答案:
【答案】(1)证明见解析;(2)6.
【解析】试题分析:(1)根据三角形的中位线平行于第三边并且等于第三边的一半可得EF∥BC且EF=![]() BC,DG∥BC且DG=
BC,DG∥BC且DG=![]() BC,从而得到DE=EF,DG∥EF,再利用一组对边平行且相等的四边形是平行四边形证明即可;
BC,从而得到DE=EF,DG∥EF,再利用一组对边平行且相等的四边形是平行四边形证明即可;
(2)先判断出∠BOC=90°,再利用直角三角形斜边的中线等于斜边的一半,求出EF即可.
试题解析:(1)∵D、G分别是AB、AC的中点,∴DG∥BC,DG=![]() BC,∵E、F分别是OB、OC的中点,∴EF∥BC,EF=
BC,∵E、F分别是OB、OC的中点,∴EF∥BC,EF=![]() BC,∴DE=EF,DG∥EF,∴四边形DEFG是平行四边形;
BC,∴DE=EF,DG∥EF,∴四边形DEFG是平行四边形;
(2)∵∠OBC和∠OCB互余,∴∠OBC+∠OCB=90°,∴∠BOC=90°,∵M为EF的中点,OM=3,∴EF=2OM=6.
由(1)有四边形DEFG是平行四边形,∴DG=EF=6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列语句中正确的是( )
A.两个三角形的面积相等,那么这两个三角形全等
B.三个内角对应相等的两个三角形全等
C.两个等腰直角三角形全等,那么它们的斜边相等
D.两边及其中一边所对的角对应相等的两个三角形全等
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,对角线AC,BD相交于点O,点E,F分别在OA,OC上
(1)给出以下条件;①OB=OD,②∠1=∠2,③OE=OF,请你从中选取两个条件证明△BEO≌△DFO;
(2)在(1)条件中你所选条件的前提下,添加AE=CF,求证:四边形ABCD是平行四边形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】6张如图所示的长为a,宽为b(a>b)的小长方形纸片,按图2的方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影部分表示,设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a、b满足( )

A.
 B.
B. 
C.
 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC 中,已知,∠A:∠B:∠C = 1:2:3,△ABC 的形状是____________________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,连接ED,DG.
(1)请判断四边形EBGD的形状,并说明理由;
(2)若∠ABC=30°,∠C=45°,ED=2
 ,点H是BD上的一个动点,求HG+HC的最小值.
,点H是BD上的一个动点,求HG+HC的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】折叠三角形纸片ABC,使点A落在BC边上的点F,且折痕DE∥BC,若∠A=75°,∠C=60°,则∠BDF=____________________________
相关试题

