搜索
【题目】已知A＝a2﹣2b2+2ab﹣3，B＝2a2﹣b2﹣
ab﹣
．
(1)求2(A+B)﹣3(2A﹣B)的值(结果用化简后的a、b的式子表示)；
(2)当
与b2互为相反数时，求(1)中式子的值．
参考答案：
【答案】(1)6a2+3b2﹣10ab+11；(2)
．
【解析】
（1）根据整式的混合运算法则计算；
（2）根据非负数的性质求出a、b，代入计算．
解：(1)2(A+B)﹣3(2A﹣B)
＝2A+2B﹣6A+3B
＝﹣4A+5B
＝﹣4(a2﹣2b2+2ab﹣3)+5(2a2﹣b2﹣
ab﹣
)
＝﹣4a2+8b2﹣8ab+12+10a2﹣5b2﹣2ab﹣1
＝6a2+3b2﹣10ab+11；
(2)∵|a+
|与b2互为相反数，
∴|a+|+b2＝0，
则a＝﹣，b＝0，
6a2+3b2﹣10ab+11＝6×
+11＝．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在数轴上点A表示﹣3，点B表示5，点C表示m.
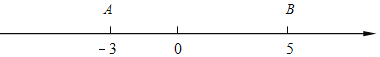
(1)若点A与点B同时出发沿数轴负方向运动，两点在点C处相遇，点A的运动速度为1单位长度/秒，点B的运动速度为3单位长度/秒，求m.
(2)若A，C两点之间的距离为2，求B、C两点之间的距离.
(3)若m＝0，在数轴上是否存在一点P，使P到A、B、C的距离和等于12？若存在，请求点P对应的数；若不存在，请说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，在等边三角形ABC中，BC＝8cm，射线AG∥BC，点E从点A出发沿射线AG以1cm/s的速度运动，同时点F从点B出发沿射线BC以2cm/s的速度运动，设运动时间为t（s）．
（1）连接EF，当EF经过AC边的中点D时，求证：四边形AFCE是平行四边形；
（2）填空：①当t为 s时，四边形ACFE是菱形；②当t为 s时，△ACE的面积是△ACF的面积的2倍．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）（操作发现）：如图一，在矩形ABCD中，E是BC的中点，将△ABE沿AE折叠后得到△AFE，点F在矩形ABCD内部，延长AF交CD于点G．猜想线段GF与GC的数量关系是 ．
（2）（类比探究）：如图二，将（1）中的矩形ABCD改为平行四边形，其它条件不变，（1）中的结论是否仍然成立？请说明理由．
（3）（应用）：如图三，将（1）中的矩形ABCD改为正方形，边长AB＝4，其它条件不变，求线段GC的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某社区准备在甲乙两位射箭爱好者中选出一人参加集训，两人各射了5箭，他们的总成绩（单位：环）相同，小宇根据他们的成绩绘制了尚不完整的统计图表（如图），并计算了甲成绩的平均数和方差（见如图小宇的作业）．
甲、乙两人射箭成绩统计表
第1次
第2次
第3次
第4次
第5次
甲成绩
9
4
7
4
6
乙成绩
7
5
7
a
7
（1）a＝ ；
（2）请完成图中表示乙成绩变化情况的折线．
（3）观察图，可看出 的成绩比较稳定（填“甲”或“乙”）．参照小宇的计算方法，计算乙成绩的方差，并验证你的判断．
-
科目： 来源： 题型：
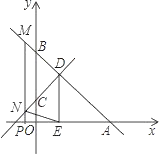
查看答案和解析>>【题目】直线y＝﹣x+6与x轴交于A，与y轴交于B，直线CD与y轴交于C（0，2）与直线AB交于D，过D作DE⊥x轴于E（2，0）．
（1）求直线CD的函数解析式；
（2）P是x轴上一动点，过P作x轴的垂线，分别与直线AB，CD交于M，N，设MN的长为d，P点的横坐标为t，求出d与t之间的函数关系式；
（3）在（2）的条件下，当t为何值时，以M，N，E，D为顶点的四边形是平行四边形．（直接写出结果）
-
科目： 来源： 题型：
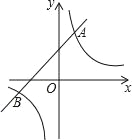
查看答案和解析>>【题目】如图，一次函数y1=kx+b（k≠0）与反比例函数y2=
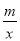（m≠0）相交于A和B两点．且A点坐标为（1，3），B点的横坐标为﹣3．（1）求反比例函数和一次函数的解析式；
（2）根据图象直接写出使得y1≤y2时，x的取值范围．
相关试题
